Search any question & find its solution
Question:
Answered & Verified by Expert
Consider the following reaction,
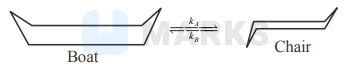
The reaction is of first order in each diagram, with an equilibrium constant of $10^{4}$. For the conversion of chair form to boat form $\mathrm{e}^{-E a / R T}=$ $4.35 \times 10^{-8} \mathrm{~m}$ at $298 \mathrm{~K}$ with pre-exponential factor of $10^{12} \mathrm{~s}^{-1}$. Apparent rate constant $(=k A / k B)$ at $298 \mathrm{~K}$ is
Options:
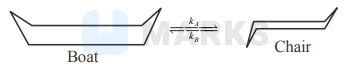
The reaction is of first order in each diagram, with an equilibrium constant of $10^{4}$. For the conversion of chair form to boat form $\mathrm{e}^{-E a / R T}=$ $4.35 \times 10^{-8} \mathrm{~m}$ at $298 \mathrm{~K}$ with pre-exponential factor of $10^{12} \mathrm{~s}^{-1}$. Apparent rate constant $(=k A / k B)$ at $298 \mathrm{~K}$ is
Solution:
1356 Upvotes
Verified Answer
The correct answer is:
$4.35 \times 10^{8} \mathrm{~s}^{-1}$
$\begin{aligned}
& \mathrm{K}_{\mathrm{B}}=\mathrm{Ae}^{-\mathrm{E}_{\mathrm{a}} / \mathrm{RT}} \\
&=10^{12} \times 4.35 \times 10^{-8} \\
&=4.35 \times 10^{4} \mathrm{~s}^{-1}
\end{aligned}$
Also equilibrium constant,
$\mathrm{k}=\frac{\mathrm{k}_{\mathrm{A}}}{\mathrm{k}_{\mathrm{B}}}=10^{4}$
$\therefore \mathrm{k}_{\mathrm{A}}=\mathrm{k}_{\mathrm{B}} \times 10^{4}=4.35 \times 10^{8} \mathrm{~s}^{-1}$
& \mathrm{K}_{\mathrm{B}}=\mathrm{Ae}^{-\mathrm{E}_{\mathrm{a}} / \mathrm{RT}} \\
&=10^{12} \times 4.35 \times 10^{-8} \\
&=4.35 \times 10^{4} \mathrm{~s}^{-1}
\end{aligned}$
Also equilibrium constant,
$\mathrm{k}=\frac{\mathrm{k}_{\mathrm{A}}}{\mathrm{k}_{\mathrm{B}}}=10^{4}$
$\therefore \mathrm{k}_{\mathrm{A}}=\mathrm{k}_{\mathrm{B}} \times 10^{4}=4.35 \times 10^{8} \mathrm{~s}^{-1}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.