Search any question & find its solution
Question:
Answered & Verified by Expert
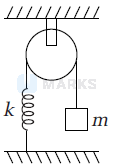
Figure shows spring + block + pulley system which are light. The time period of mass would be
Options:

Solution:
2808 Upvotes
Verified Answer
The correct answer is:
$2 \pi \sqrt{\frac{m}{k}}$
Let when $m$ is hanging, the extension in the spring is $l$, then tension in the string is,
$T_1=k l=m g$
when force is applied, let the further extension is x . The tension in the spring is
$T_2=k(x+l)$
$\begin{aligned} & \therefore \text { Driving force }=T_2-T_1=k(x+l)-k l=k x \\ & \therefore \text { Acceleration }=\frac{k l}{m}\end{aligned}$
$\begin{aligned} \Rightarrow \quad T & =2 \pi \sqrt{\frac{\text { displacement }}{\text { acceleration }}} \\ & =2 \pi \sqrt{\frac{x}{\frac{k x}{m}}}=2 \pi \sqrt{\frac{m}{k}}\end{aligned}$
$T_1=k l=m g$
when force is applied, let the further extension is x . The tension in the spring is
$T_2=k(x+l)$
$\begin{aligned} & \therefore \text { Driving force }=T_2-T_1=k(x+l)-k l=k x \\ & \therefore \text { Acceleration }=\frac{k l}{m}\end{aligned}$
$\begin{aligned} \Rightarrow \quad T & =2 \pi \sqrt{\frac{\text { displacement }}{\text { acceleration }}} \\ & =2 \pi \sqrt{\frac{x}{\frac{k x}{m}}}=2 \pi \sqrt{\frac{m}{k}}\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.