Search any question & find its solution
Question:
Answered & Verified by Expert
For a particle executing simple harmonic motion, the displacement-time $(x-t)$ graph is as shown in the figure. The acceleration of the particle at $t=\frac{4}{3} \mathrm{~s}$ is
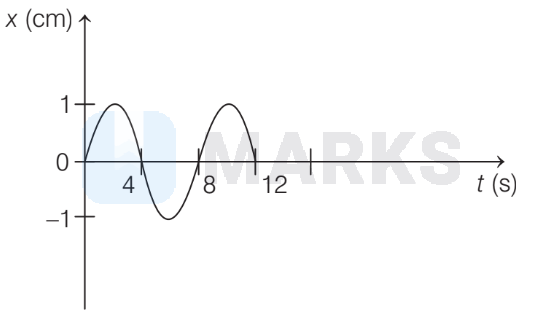
Options:

Solution:
1578 Upvotes
Verified Answer
The correct answer is:
$-\frac{\sqrt{3}}{32} \pi^2 \mathrm{~cm} \mathrm{~s}^{-2}$
The displacement-time graph shown in the figure is a sine wave, so the equation of displacement, $x=1 \sin \omega t$
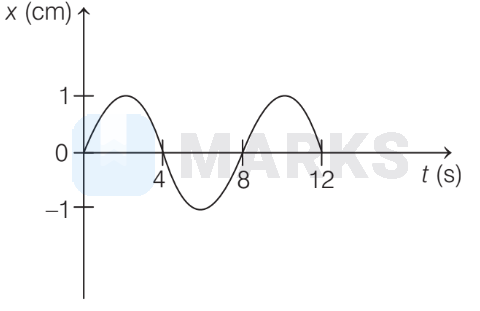
Here, $\quad T=8 \mathrm{~s}$
(for a complete cycle)
Hence, $\omega=\frac{2 \pi}{T}=\frac{2 \pi}{8}=\frac{\pi}{4} \mathrm{rad} / \mathrm{s}$
and acceleration in SHM,
$$
\begin{aligned}
\alpha & =-\omega^2 a \sin \omega t \\
\alpha & =-\left(\frac{\pi}{4}\right)^2 \times 1 \times \sin \left(\frac{\pi}{4} \times \frac{4}{3}\right) \\
\Rightarrow \quad \alpha & =-\frac{\pi^2}{16} \times \frac{\sqrt{3}}{2}=-\frac{\pi^2 \sqrt{3}}{32} \mathrm{~cm} \mathrm{~s}^{-2}
\end{aligned}
$$
Hence, the correct option is (a).

Here, $\quad T=8 \mathrm{~s}$
(for a complete cycle)
Hence, $\omega=\frac{2 \pi}{T}=\frac{2 \pi}{8}=\frac{\pi}{4} \mathrm{rad} / \mathrm{s}$
and acceleration in SHM,
$$
\begin{aligned}
\alpha & =-\omega^2 a \sin \omega t \\
\alpha & =-\left(\frac{\pi}{4}\right)^2 \times 1 \times \sin \left(\frac{\pi}{4} \times \frac{4}{3}\right) \\
\Rightarrow \quad \alpha & =-\frac{\pi^2}{16} \times \frac{\sqrt{3}}{2}=-\frac{\pi^2 \sqrt{3}}{32} \mathrm{~cm} \mathrm{~s}^{-2}
\end{aligned}
$$
Hence, the correct option is (a).
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.