Search any question & find its solution
Question:
Answered & Verified by Expert
Four identical cells of emf \( E \) and internal resistance \( r \) are to be connected in series. Suppose if
one of the cell is connected wrongly, the equivalent emf and effective internal resistance of the
combination is
Options:
one of the cell is connected wrongly, the equivalent emf and effective internal resistance of the
combination is
Solution:
2280 Upvotes
Verified Answer
The correct answer is:
\( 2 \mathrm{E} \) and \( 4 \mathrm{r} \)
When all the cells are connected correctly, then
Equivalent emf = 4E and effective resistance \( =4 r \)
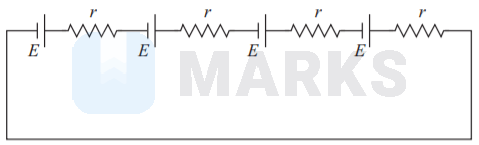
If one of the cell is connected wrongly then, effective internal resistance will remain unchanged while, equivalent emf is
\( E^{\prime}=E(n-2 m) \)
where \( n \) is total number of cells; \( m \) is number of wrongly connected cells.
Therefore,
\( E=E(4-2 \times 1)=E(4-2)=2 E \)
\( \Rightarrow \) equivalent emf \( =2 \mathrm{E} \) and effective internal resistance \( =4 \mathrm{r} \)
Equivalent emf = 4E and effective resistance \( =4 r \)

If one of the cell is connected wrongly then, effective internal resistance will remain unchanged while, equivalent emf is
\( E^{\prime}=E(n-2 m) \)
where \( n \) is total number of cells; \( m \) is number of wrongly connected cells.
Therefore,
\( E=E(4-2 \times 1)=E(4-2)=2 E \)
\( \Rightarrow \) equivalent emf \( =2 \mathrm{E} \) and effective internal resistance \( =4 \mathrm{r} \)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.