If $3 x+y+k=0$ is a tangent to the circle $x^2+y^2=10$, then $k=\ldots . . .$.

Question

If $3 x+y+k=0$ is a tangent to the circle $x^2+y^2=10$, then $k=\ldots . . .$., \pm 7, \pm 5, \pm 9, \pm 10

MARKS App · Accepted Answer

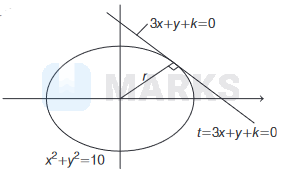
Length of perpendicular from $(0,0)$ on $3 x+y+k=0$ $=$ radius of circle. $\Rightarrow\left|\frac{3 \times 0+0+k}{\sqrt{3^2+12}}\right|=\sqrt{10} \Rightarrow \frac{k}{\sqrt{10}}= \pm \sqrt{10}$ $\Rightarrow \quad k= \pm(\sqrt{10})^2 \Rightarrow k= \pm 10$

Search any question & find its solution

Looking for more such questions to practice?