Search any question & find its solution
Question:
Answered & Verified by Expert
If $\vec{a}$ and $\vec{b}$ are the position vectors of $\vec{A}$ and $\vec{B}$ respectively, then find the position vector of a point $\vec{C}$ in $\overrightarrow{\mathrm{BA}}$ produced such that $\overrightarrow{\mathrm{BC}}=1.5 \overrightarrow{\mathrm{BA}}$.
Solution:
2702 Upvotes
Verified Answer
$\therefore \overrightarrow{\mathrm{BA}}=\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}}$
and $1.5 \overrightarrow{\mathrm{BA}}=1.5(\overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}})$
Since, $\overline{\mathrm{BC}}=1.5 \overrightarrow{\mathrm{BA}}=1.5(\overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}})$
$\overline{\mathrm{OC}}-\overline{\mathrm{OB}}=1.5 \overrightarrow{\mathrm{a}}-1.5 \overrightarrow{\mathrm{b}}$
$\overrightarrow{\mathrm{OC}}=1.5 \overrightarrow{\mathrm{a}}-1.5 \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}}$
$=1.5 \vec{a}-0.5 \vec{b}$
$[\because \overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{b}}]$
$=\frac{3 \vec{a}-\vec{b}}{2}$
Graphically
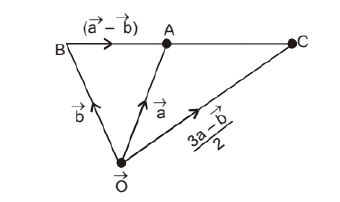
and $1.5 \overrightarrow{\mathrm{BA}}=1.5(\overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}})$
Since, $\overline{\mathrm{BC}}=1.5 \overrightarrow{\mathrm{BA}}=1.5(\overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}})$
$\overline{\mathrm{OC}}-\overline{\mathrm{OB}}=1.5 \overrightarrow{\mathrm{a}}-1.5 \overrightarrow{\mathrm{b}}$
$\overrightarrow{\mathrm{OC}}=1.5 \overrightarrow{\mathrm{a}}-1.5 \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}}$
$=1.5 \vec{a}-0.5 \vec{b}$
$[\because \overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{b}}]$
$=\frac{3 \vec{a}-\vec{b}}{2}$
Graphically

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.