Search any question & find its solution
Question:
Answered & Verified by Expert
If $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are lengths of the sides $\mathrm{BC}, \mathrm{CA}, \mathrm{AB}$ respectively of $\triangle \mathrm{ABC}$ and $\mathrm{H}$ is any
point in the plane of $\Delta \mathrm{ABC}$ such that a $\overline{A H}+b \overline{B H}+c \overline{C H}=\overline{0}$, then $\mathrm{H}$ is the
Options:
point in the plane of $\Delta \mathrm{ABC}$ such that a $\overline{A H}+b \overline{B H}+c \overline{C H}=\overline{0}$, then $\mathrm{H}$ is the
Solution:
2163 Upvotes
Verified Answer
The correct answer is:
Incentre of $\Delta \mathrm{ABC}$
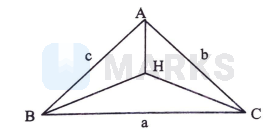
Consider $\mathrm{H}$ to be origin.
Then position vector of the vertices $A, B, C$ are $\bar{a}, \bar{b}, \bar{c}$ respectively.
We have $\mathrm{a} \overline{\mathrm{AH}}+\mathrm{b} \overline{\mathrm{BH}}+\mathrm{c} \overline{\mathrm{CH}}=\overline{0}$ i.e. $\quad \mathrm{a} \overline{\mathrm{a}}+\mathrm{b} \overline{\mathrm{b}}+\mathrm{c} \overline{\mathrm{c}}=0$
i.e. $\frac{a \bar{a}+b \bar{b}+c \bar{c}}{a+b+c}=0$, which is position vector of incentre.
Hence $\mathrm{H}$ is incentre of triangle.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.