Search any question & find its solution
Question:
Answered & Verified by Expert
If $\quad \overrightarrow{\mathbf{a}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}, \overrightarrow{\mathbf{b}}=\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}, \quad \overrightarrow{\mathbf{c}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}}$ and $\overrightarrow{\mathbf{d}}=\hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}}$, then observe the following
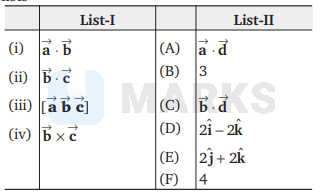
The correct match of List-I to List-II
$\begin{array}{llll}\text { i } & \text { ii } & \text { iii } & \text { iv }\end{array}$
Options:

The correct match of List-I to List-II
$\begin{array}{llll}\text { i } & \text { ii } & \text { iii } & \text { iv }\end{array}$
Solution:
1322 Upvotes
Verified Answer
The correct answer is:
$\begin{array}{llll}\text { C } & \text { A } & \text { F } & \text { E }\end{array}$
Given vectors are
$$
\begin{aligned}
\overrightarrow{\mathbf{a}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}, \overrightarrow{\mathbf{b}} & =\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}, \overrightarrow{\mathbf{c}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}} \\
\text { and } \quad \overrightarrow{\mathbf{d}} & =\hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}}
\end{aligned}
$$
and
$$
\overrightarrow{\mathbf{d}}=\hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}}
$$
$$
\text { (i) Now, } \begin{aligned}
\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}} & =(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}) \cdot(\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}) \\
& =1-1+1=1 \\
\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{d}} & =(\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}) \cdot(\hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}}) \\
& =1+1-1=1 \\
\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}} & =\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{d}}
\end{aligned}
$$
(ii)
$$
\text { (ii) Now, } \begin{aligned}
\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{c}} & =(\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}) \cdot(\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}}) \\
& =1-1-1=-1 \\
\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{d}} & =(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}) \cdot(\hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}}) \\
& =1-1-1=-1 \\
\therefore \quad \overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{c}} & =\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{d}}
\end{aligned}
$$
$$
\text { (iii) } \begin{aligned}
{\left[\begin{array}{ll}
\overrightarrow{\mathbf{a}} \overrightarrow{\mathbf{b}} \overrightarrow{\mathbf{c}}
\end{array}\right] } & =\left|\begin{array}{rrr}
1 & 1 & 1 \\
1 & -1 & 1 \\
1 & 1 & -1
\end{array}\right| \\
& =1(1-1)-1(-1-1)+1(1+1) \\
& =0+2+2=4
\end{aligned}
$$
(iv)
$$
\begin{aligned}
\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}} & =\left|\begin{array}{rrr}
\hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\
1 & -1 & 1 \\
1 & 1 & -1
\end{array}\right| \\
& =\hat{\mathbf{i}}(1-1)-\hat{\mathbf{j}}(-1-1)+\hat{\mathbf{k}}(1+1) \\
& =2 \hat{\mathbf{j}}+2 \hat{\mathbf{k}}
\end{aligned}
$$
Hence, option (2) is correct.
$$
\begin{aligned}
\overrightarrow{\mathbf{a}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}, \overrightarrow{\mathbf{b}} & =\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}, \overrightarrow{\mathbf{c}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}} \\
\text { and } \quad \overrightarrow{\mathbf{d}} & =\hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}}
\end{aligned}
$$
and
$$
\overrightarrow{\mathbf{d}}=\hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}}
$$
$$
\text { (i) Now, } \begin{aligned}
\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}} & =(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}) \cdot(\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}) \\
& =1-1+1=1 \\
\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{d}} & =(\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}) \cdot(\hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}}) \\
& =1+1-1=1 \\
\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}} & =\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{d}}
\end{aligned}
$$
(ii)
$$
\text { (ii) Now, } \begin{aligned}
\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{c}} & =(\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}) \cdot(\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}}) \\
& =1-1-1=-1 \\
\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{d}} & =(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}) \cdot(\hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}}) \\
& =1-1-1=-1 \\
\therefore \quad \overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{c}} & =\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{d}}
\end{aligned}
$$
$$
\text { (iii) } \begin{aligned}
{\left[\begin{array}{ll}
\overrightarrow{\mathbf{a}} \overrightarrow{\mathbf{b}} \overrightarrow{\mathbf{c}}
\end{array}\right] } & =\left|\begin{array}{rrr}
1 & 1 & 1 \\
1 & -1 & 1 \\
1 & 1 & -1
\end{array}\right| \\
& =1(1-1)-1(-1-1)+1(1+1) \\
& =0+2+2=4
\end{aligned}
$$
(iv)
$$
\begin{aligned}
\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}} & =\left|\begin{array}{rrr}
\hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\
1 & -1 & 1 \\
1 & 1 & -1
\end{array}\right| \\
& =\hat{\mathbf{i}}(1-1)-\hat{\mathbf{j}}(-1-1)+\hat{\mathbf{k}}(1+1) \\
& =2 \hat{\mathbf{j}}+2 \hat{\mathbf{k}}
\end{aligned}
$$
Hence, option (2) is correct.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.