Search any question & find its solution
Question:
Answered & Verified by Expert
If a line is moving between the coordinate axes such that the sum of the intercepts made by it on the coordinate axes is always 12 , then the equation of that line which forms a triangle of maximum area with the coordinate axes is
Options:
Solution:
1939 Upvotes
Verified Answer
The correct answer is:
$x+y=6$
Given $a+b=12$
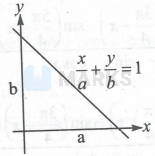
Now, Area of triangle (A) $=\frac{1}{2} a b$
$\Rightarrow A=\frac{1}{2} a(12-a)$
Since, $\frac{d A}{d a}=\frac{12-2 a}{2}=b-a$ for $\max$ of $A, \frac{d A}{d a}=0 \Rightarrow a=b$
So $b=12-6=6$
So equation of line $\frac{x}{6}+\frac{y}{6}=1 \Rightarrow x+y=6$

Now, Area of triangle (A) $=\frac{1}{2} a b$
$\Rightarrow A=\frac{1}{2} a(12-a)$
Since, $\frac{d A}{d a}=\frac{12-2 a}{2}=b-a$ for $\max$ of $A, \frac{d A}{d a}=0 \Rightarrow a=b$
So $b=12-6=6$
So equation of line $\frac{x}{6}+\frac{y}{6}=1 \Rightarrow x+y=6$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.