Search any question & find its solution
Question:
Answered & Verified by Expert
If a number is chosen at random from out of the four digited numbers formed by using the digits $0,1,2,3,4,6$ without repetition, then the probability that it is divisible by 4 , is
Options:
Solution:
2037 Upvotes
Verified Answer
The correct answer is:
$\frac{17}{50}$
If the number divisible by 4 using digits 0,1 , $2,3,4,6$ unit place digit is even.
Case I. If unit digit is 0 , then tens place possible digits is $2,4,6$
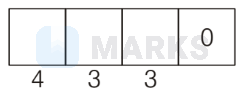
Possible outcome $=4 \times 3 \times 3=36$
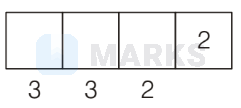
Case II. If unit digit is 2 , then tens place digits are 1 and 3
Possible outcomes
$$
=3 \times 3 \times 2=18
$$
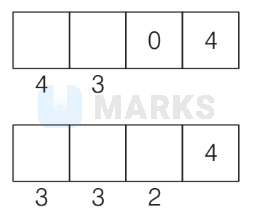
Case III. If unit digit is 4 , then tens digits are 0,2 and 6 .
(a) If tens digit 0
Possible ways
$$
=4 \times 3=12
$$
(b) If tens digit not zero, i.e.
(2 and 6)
Possible ways
$$
=3 \times 3 \times 2=18
$$
So, required ways, if unit digit is $4=18+12=30$.
Case IV. If unit digit is 6 , then digit are 1 and 3 Possible ways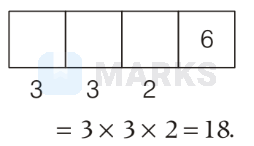
Hence, total number of number which is divisible by $4=36+18+30+18$ $=102$
Now, total number of ways of form four digit number using $0,1,2,3,4,6$ is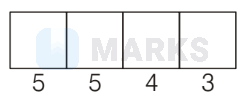
Total number of 4 digit number
$$
\begin{array}{r}
=5 \times 5 \times 4 \times 3=300 \\
\therefore \text { Required probability }=\frac{102}{300}=\frac{17}{50}
\end{array}
$$
Case I. If unit digit is 0 , then tens place possible digits is $2,4,6$

Possible outcome $=4 \times 3 \times 3=36$
Case II. If unit digit is 2 , then tens place digits are 1 and 3
Possible outcomes
$$
=3 \times 3 \times 2=18
$$

Case III. If unit digit is 4 , then tens digits are 0,2 and 6 .
(a) If tens digit 0
Possible ways
$$
=4 \times 3=12
$$
(b) If tens digit not zero, i.e.
(2 and 6)
Possible ways
$$
=3 \times 3 \times 2=18
$$

So, required ways, if unit digit is $4=18+12=30$.
Case IV. If unit digit is 6 , then digit are 1 and 3 Possible ways

Hence, total number of number which is divisible by $4=36+18+30+18$ $=102$
Now, total number of ways of form four digit number using $0,1,2,3,4,6$ is
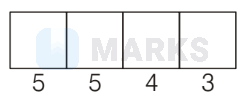
Total number of 4 digit number
$$
\begin{array}{r}
=5 \times 5 \times 4 \times 3=300 \\
\therefore \text { Required probability }=\frac{102}{300}=\frac{17}{50}
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.