Search any question & find its solution
Question:
Answered & Verified by Expert
If a ray of light in denser medium strikes a rarer medium at angle of incidence $i$, the angles of reflection and refraction are $r$ and $r^{\prime}$ respectively. If the reflected and refracted rays are at right angles to each other, the critical angle for the given pair of media is
Options:
Solution:
2544 Upvotes
Verified Answer
The correct answer is:
$\tan ^{-1}(\sin \mathrm{i})$
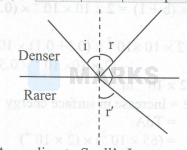
According to Snell's Law,
$\begin{array}{ll}
& \frac{\sin i}{\sin r}=\frac{1}{n} \\
& \text { But } i=r, \\
\therefore \quad & \frac{\sin r}{\sin r^{\prime}}=\frac{1}{n} \\
& \text { From figure } r^{\prime}+r+90=180^{\circ} \\
\therefore \quad & r^{\prime}=180^{\circ}-90^{\circ}-r=90^{\circ}-r \\
\therefore \quad & \Rightarrow \frac{\sin r}{\sin \left(90^{\circ}-r\right)}=\frac{1}{n} \\
& \frac{\sin r}{\cos r}=\frac{1}{n}
\end{array}$
$\therefore \quad \tan \mathrm{r}=\frac{1}{\mathrm{n}}$
Critical angle is given by $\sin i_c=\frac{1}{n}$
$\begin{array}{ll}
\therefore & \tan r=\sin i_c \\
\therefore & i_c=\sin ^{-1}(\tan r)
\end{array}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.