Search any question & find its solution
Question:
Answered & Verified by Expert
If a straight line $y-x=2$ divides the region $x^2+y^2 \leq 4$ into two parts, then the ratio of the area of the smaller part to the area of the greater part is
Options:
Solution:
1552 Upvotes
Verified Answer
The correct answer is:
$\pi-2: 3 \pi+2$
$\pi-2: 3 \pi+2$
Let I be the smaller portion and II be the greater portion of the given figure then,
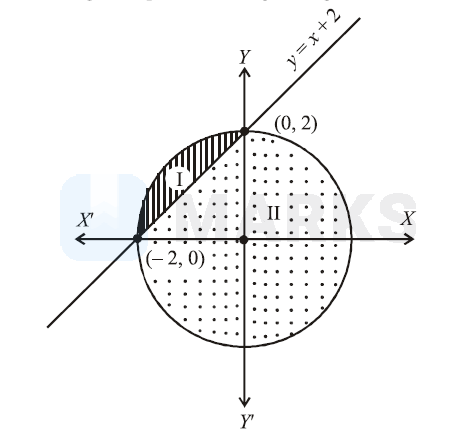
Area of $I=\int_{-2}^0\left[\sqrt{4-x^2}-(x+2] d x\right.$
$$
\begin{aligned}
& =\left[\frac{x}{2} \sqrt{4-x^2}+\frac{4}{2} \sin ^{-1}\left(\frac{x}{2}\right)\right]_{-2}^0-\left[\frac{x^2}{2}+2 x\right]_{-2}^0 \\
& =\left[2 \sin ^{-1}(-1)\right]-\left[-\frac{4}{2}+4\right]=2 \times \frac{\pi}{2}-2=\pi-2
\end{aligned}
$$
Now, area of $\mathrm{II}=$ Area of circle $-$ area of $\mathrm{I}$.
$$
\begin{aligned}
& =4 \pi-(\pi-2) \\
& =3 \pi+2
\end{aligned}
$$
Hence, required ratio $=\frac{\text { area of I }}{\text { area of II }}=\frac{\pi-2}{3 \pi+2}$

Area of $I=\int_{-2}^0\left[\sqrt{4-x^2}-(x+2] d x\right.$
$$
\begin{aligned}
& =\left[\frac{x}{2} \sqrt{4-x^2}+\frac{4}{2} \sin ^{-1}\left(\frac{x}{2}\right)\right]_{-2}^0-\left[\frac{x^2}{2}+2 x\right]_{-2}^0 \\
& =\left[2 \sin ^{-1}(-1)\right]-\left[-\frac{4}{2}+4\right]=2 \times \frac{\pi}{2}-2=\pi-2
\end{aligned}
$$
Now, area of $\mathrm{II}=$ Area of circle $-$ area of $\mathrm{I}$.
$$
\begin{aligned}
& =4 \pi-(\pi-2) \\
& =3 \pi+2
\end{aligned}
$$
Hence, required ratio $=\frac{\text { area of I }}{\text { area of II }}=\frac{\pi-2}{3 \pi+2}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.