Search any question & find its solution
Question:
Answered & Verified by Expert
If an electron in hydrogen atom jumps from $3^{\text {rd }}$ orbit to $2^{\text {nd }}$ orbit, it emits a photon of wavelength ' $\lambda$ '. When it jumps from $4^{\text {th }}$ orbit to $3^{\text {rd }}$ orbit, the corresponding wavelength of the photon will be
Options:
Solution:
1406 Upvotes
Verified Answer
The correct answer is:
$\frac{20}{7} \lambda$
Rydberg's relation is given by
$\frac{1}{\lambda}=\mathrm{R}_{\mathrm{H}} \mathrm{Z}^2\left(\frac{1}{\mathrm{n}_1^2}-\frac{1}{\mathrm{n}_2^2}\right)$
For hydrogen, $\mathrm{Z}=1$.
Given, for $3^{\text {rd }}$ to $2^{\text {nd }}$ orbit transition
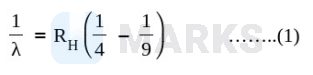
And for $4^{\text {th }}$ to $3^{\text {rd }}$ orbit transition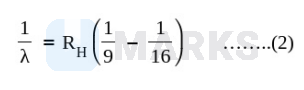
Taking ratio of eqn (1) \& (2)
$\begin{aligned}
& \frac{\lambda_n}{\lambda}=\frac{5}{36} \times \frac{(16 \times 9)}{7}=\frac{20}{7} \\
& \Rightarrow \lambda_n=\frac{20}{7} \lambda
\end{aligned}$
$\frac{1}{\lambda}=\mathrm{R}_{\mathrm{H}} \mathrm{Z}^2\left(\frac{1}{\mathrm{n}_1^2}-\frac{1}{\mathrm{n}_2^2}\right)$
For hydrogen, $\mathrm{Z}=1$.
Given, for $3^{\text {rd }}$ to $2^{\text {nd }}$ orbit transition
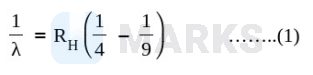
And for $4^{\text {th }}$ to $3^{\text {rd }}$ orbit transition
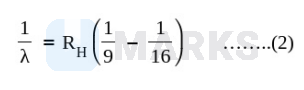
Taking ratio of eqn (1) \& (2)
$\begin{aligned}
& \frac{\lambda_n}{\lambda}=\frac{5}{36} \times \frac{(16 \times 9)}{7}=\frac{20}{7} \\
& \Rightarrow \lambda_n=\frac{20}{7} \lambda
\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.