Given, $\cot A=\frac{11}{60}$
$\therefore \tan A=\frac{60}{11}$ and $\cos B=\frac{7}{25}$


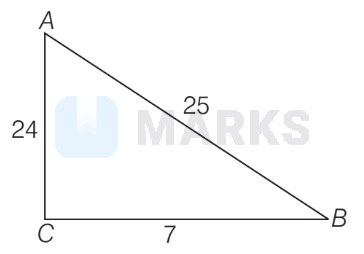
$\begin{aligned} & \because A \text { and } B \notin Q_1 \\ & \therefore A \in Q_3 \text { and } B \in Q_4 \\ & \therefore \tan B=-\frac{24}{7} \quad\left(\because \tan B=\text { negative in } Q_4\right) \\ & \Rightarrow \frac{2 \tan \frac{B}{2}}{1-\tan ^2 \frac{B}{2}}=-\frac{24}{7} \\ & \Rightarrow 12 \tan ^2 \frac{B}{2}-7 \tan \frac{B}{2}-12=0 \\ & \Rightarrow\left(3 \tan ^{\frac{B}{2}}-4\right)\left(4 \tan \frac{B}{2}+3\right)=0 \\ & \Rightarrow \tan \frac{B}{2}=\frac{4}{3}(\text { Rejected }) \text { because } B \in Q_4 \text { i.e. } \\ & \frac{3 \pi}{2} < B < 2 \pi \\ & \therefore \quad \frac{3 \pi}{4} < \frac{B}{2} < \pi \\ & \text { i.e. } \quad \frac{B}{2} \in Q_2 \\ & \therefore \quad \tan \frac{B}{2}=\text { negative } \\ & \text { or } \quad \tan \frac{B}{2}=-\frac{3}{4}\end{aligned}$
$\begin{aligned} & \text { Now, } \tan \left(A+\frac{B}{2}\right)=\frac{\tan A+\tan \frac{B}{2}}{1-\tan A \cdot \tan \frac{B}{2}} \\ & =\frac{\frac{60}{11}-\frac{3}{4}}{1-\frac{60}{11}\left(-\frac{3}{4}\right)} \\ & =\frac{\frac{240-33}{44}}{\frac{224}{44}}=\frac{207}{224} \\ & \therefore\left(A+\frac{B}{2}\right) \in Q_1 \\ & \end{aligned}$