Search any question & find its solution
Question:
Answered & Verified by Expert
If $f: \mathbf{R} \rightarrow \mathbf{R}$ be defined by
$f(x)=x+2|x+1|+2|x-1|$, then the element in the co-domain, which has unique pre image in the domain is
Options:
$f(x)=x+2|x+1|+2|x-1|$, then the element in the co-domain, which has unique pre image in the domain is
Solution:
1545 Upvotes
Verified Answer
The correct answer is:
3
We have,
$\begin{aligned}
& f(x)=x+2|x+1|+2|x-1| \\
& f(x)=\left\{\begin{array}{cc}
x+2(-x-1)+2(-x+1), & x \leq-1 \\
x+2(x+1)+2(-x+1), & -1 < x \leq 1 \\
x+2(x+1)+2(x-1), & x \geq 1
\end{array}\right. \\
& f(x)=\left\{\begin{array}{cc}
-3 x, & x \leq-1 \\
x+4, & -1 < x < 1 \\
5 x, & x \geq 1
\end{array}\right.
\end{aligned}$
Graph of $f(x)$ is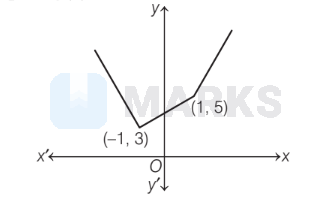
Clearly, 3 has unique image in the domain.
$\begin{aligned}
& f(x)=x+2|x+1|+2|x-1| \\
& f(x)=\left\{\begin{array}{cc}
x+2(-x-1)+2(-x+1), & x \leq-1 \\
x+2(x+1)+2(-x+1), & -1 < x \leq 1 \\
x+2(x+1)+2(x-1), & x \geq 1
\end{array}\right. \\
& f(x)=\left\{\begin{array}{cc}
-3 x, & x \leq-1 \\
x+4, & -1 < x < 1 \\
5 x, & x \geq 1
\end{array}\right.
\end{aligned}$
Graph of $f(x)$ is

Clearly, 3 has unique image in the domain.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.