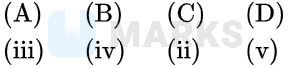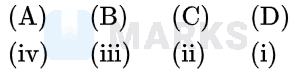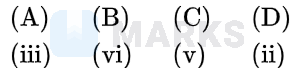Search any question & find its solution
Question:
Answered & Verified by Expert
If $f: R \rightarrow R$ is defined by
$f(x)=\left\{\begin{array}{ccc}
x+4 & \text { for } & x < -4 \\
3 x+2 & \text { for } & -4 \leq x < 4 \\
x-4 & \text { for } & x \geq 4
\end{array}\right.$
then the correct matching of List I fromList-II is :
Options:
$f(x)=\left\{\begin{array}{ccc}
x+4 & \text { for } & x < -4 \\
3 x+2 & \text { for } & -4 \leq x < 4 \\
x-4 & \text { for } & x \geq 4
\end{array}\right.$
then the correct matching of List I fromList-II is :

Solution:
1121 Upvotes
Verified Answer
The correct answer is:
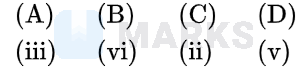
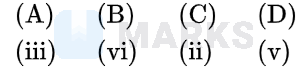
$\because \quad f(x)=\left\{\begin{array}{ccc}x+4, & \text { for } & x < -4 \\ 3 x+2, & \text { for } & -4 \leq x < 4 \\ x-4, & \text { for } & x \geq 4\end{array}\right.$
(A) $f(-5)+f(-4)=(-5+4)+(3(-4)+2)$
$=-1+(-12+2)$
$=-1-10=-11$
(B) $\quad f(|f(-8)|)=f(|-8+4|)$
$=f(4)=4-4=0$
(C) $\quad f(f(-7)+f(3))$
$=f(-7+4+9+2)$
$=f(8)=8-4=4$
(D) $f(f(f(f(0))))+1$
$=f(f(f(2)))+1$
$=f(f(6+2))+1$
$=f(f(8))+1$
$=f(8-4)+1=f(4)+1=4-4+1$
$=1$
(A) $f(-5)+f(-4)=(-5+4)+(3(-4)+2)$
$=-1+(-12+2)$
$=-1-10=-11$
(B) $\quad f(|f(-8)|)=f(|-8+4|)$
$=f(4)=4-4=0$
(C) $\quad f(f(-7)+f(3))$
$=f(-7+4+9+2)$
$=f(8)=8-4=4$
(D) $f(f(f(f(0))))+1$
$=f(f(f(2)))+1$
$=f(f(6+2))+1$
$=f(f(8))+1$
$=f(8-4)+1=f(4)+1=4-4+1$
$=1$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.