Search any question & find its solution
Question:
Answered & Verified by Expert
If $I_n=\int\left(\cos ^n x+\sin ^n x\right) d x$ and $I_n-\frac{n-1}{n} I_{n-2}$ $=\frac{\sin x \cos x}{n} f(x)$, then $f(x)=$
Options:
Solution:
2375 Upvotes
Verified Answer
The correct answer is:
$\cos ^{n-2} x-\sin ^{n-2} x$
Here, $I_n=\int\left(\cos ^n x+\sin ^n x\right) d x$
$I_n=\int \cos ^{n-1} x \cos x d x+\int \sin ^{n-1} x \sin x d x$
Using by parts,
$\begin{aligned} I_n & \left.=\cos ^{n-1} x \int \cos x d x-\int\left(\frac{d}{d x}\left(\cos ^{n-1} x\right) \int \cos x d x\right)\right) d x \\ & +\sin ^{n-1} x \int \sin x d x-\int\left(\frac{d}{d x}\left(\sin ^{n-1}\right) \int\left(\int \sin d x\right) d x\right.\end{aligned}$
$\begin{aligned} \Rightarrow I_n & =\cos ^{n-1} \sin x+\int(n-1) \cos ^{n-2} x \sin ^2 x d x \\ & -\sin ^{n-1} x \cos x+\int(n-1) \sin ^{n-2} x \cos ^2 x d x\end{aligned}$
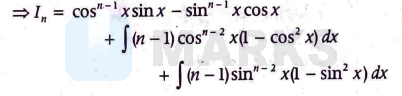
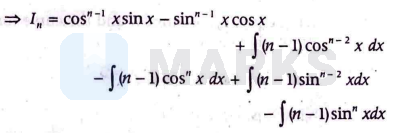
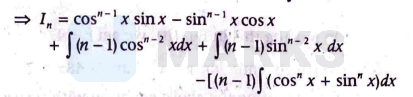
$\begin{array}{rl}\Rightarrow I_n=\cos ^{n-1} x \sin x-\sin ^{n-1} & x \cos x \\ + & (n-1) I_{n-2}-(n-1) I_n\end{array}$
$\begin{aligned} \Rightarrow I_n(1+n-1)-( & (n-1) I_{n-2} \\ & =\cos ^{n-1} x \sin x-\sin ^{n-1} x \cos x\end{aligned}$
$\begin{aligned} & \Rightarrow n\left(l_n\right)-(n-1) I_{n-2}=\cos ^{n-1} x \sin x-\sin ^{n-1} x \cos x \\ & \Rightarrow I_n-\left(\frac{n-1}{n}\right) I_{n-2}=\frac{\sin x \cos x}{n}\left(\cos ^{n-2} x-\sin ^{n-2} x\right)\end{aligned}$
$=\frac{\sin x \cos x}{n} f(x)$
$\therefore f(x)=\cos ^{n-2} x-\sin ^{n-2} x$
$I_n=\int \cos ^{n-1} x \cos x d x+\int \sin ^{n-1} x \sin x d x$
Using by parts,
$\begin{aligned} I_n & \left.=\cos ^{n-1} x \int \cos x d x-\int\left(\frac{d}{d x}\left(\cos ^{n-1} x\right) \int \cos x d x\right)\right) d x \\ & +\sin ^{n-1} x \int \sin x d x-\int\left(\frac{d}{d x}\left(\sin ^{n-1}\right) \int\left(\int \sin d x\right) d x\right.\end{aligned}$
$\begin{aligned} \Rightarrow I_n & =\cos ^{n-1} \sin x+\int(n-1) \cos ^{n-2} x \sin ^2 x d x \\ & -\sin ^{n-1} x \cos x+\int(n-1) \sin ^{n-2} x \cos ^2 x d x\end{aligned}$
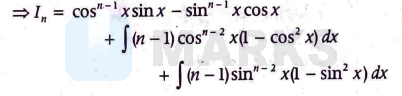
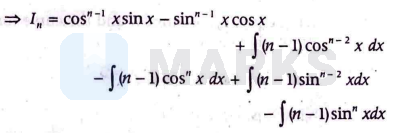
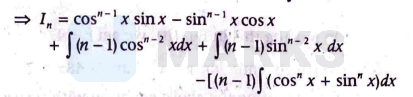
$\begin{array}{rl}\Rightarrow I_n=\cos ^{n-1} x \sin x-\sin ^{n-1} & x \cos x \\ + & (n-1) I_{n-2}-(n-1) I_n\end{array}$
$\begin{aligned} \Rightarrow I_n(1+n-1)-( & (n-1) I_{n-2} \\ & =\cos ^{n-1} x \sin x-\sin ^{n-1} x \cos x\end{aligned}$
$\begin{aligned} & \Rightarrow n\left(l_n\right)-(n-1) I_{n-2}=\cos ^{n-1} x \sin x-\sin ^{n-1} x \cos x \\ & \Rightarrow I_n-\left(\frac{n-1}{n}\right) I_{n-2}=\frac{\sin x \cos x}{n}\left(\cos ^{n-2} x-\sin ^{n-2} x\right)\end{aligned}$
$=\frac{\sin x \cos x}{n} f(x)$
$\therefore f(x)=\cos ^{n-2} x-\sin ^{n-2} x$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.