Search any question & find its solution
Question:
Answered & Verified by Expert
If in a parallelogram $\mathrm{ABDC}$, the coordinates of $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are respectively (1,2),(3,4) and $(2,5),$ then the equation of the diagonal $\mathrm{AD}$ is :
Options:
Solution:
2998 Upvotes
Verified Answer
The correct answer is:
$5 x-3 y+1=0$
Since, in parallelogram mid points of both diagonals
coinsides.
$\therefore$ mid-point of $A D=$ mid-point of $B C$
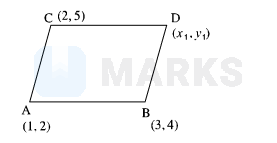
$\left(\frac{x_{1}+1}{2}, \frac{y_{1}+2}{2}\right)=\left(\frac{3+2}{2}, \frac{4+5}{2}\right)$
$\therefore \quad\left(x_{1}, y_{1}\right)=(4,7)$
Then, equation of $A D$ is,
$y-7=\frac{2-7}{1-4}(x-4)$
$y-7=\frac{5}{3}(x-4)$
$3 y-21=5 x-20$
$5 x-3 y+1=0$
coinsides.
$\therefore$ mid-point of $A D=$ mid-point of $B C$

$\left(\frac{x_{1}+1}{2}, \frac{y_{1}+2}{2}\right)=\left(\frac{3+2}{2}, \frac{4+5}{2}\right)$
$\therefore \quad\left(x_{1}, y_{1}\right)=(4,7)$
Then, equation of $A D$ is,
$y-7=\frac{2-7}{1-4}(x-4)$
$y-7=\frac{5}{3}(x-4)$
$3 y-21=5 x-20$
$5 x-3 y+1=0$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.