Search any question & find its solution
Question:
Answered & Verified by Expert
If $l$ and $m$ are the degree and the order respectively of the differential equation of the family of all circles in the $X Y$ plane with radius 5 units, then $2 l+3 m=$
Options:
Solution:
2472 Upvotes
Verified Answer
The correct answer is:
10
Family of all circles in the $x y$-planewith radius 5 units with center $\left(x_1, y_1\right)$ is
$$
\left(x-x_1\right)^2+\left(y-y_1\right)^2=5^2
$$

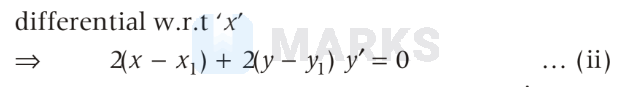
$$
\Rightarrow \quad\left(x-x_1\right)=-\left(y-y_1\right) y^{\prime}
$$
Now Eq. (ii) diff again w.r.t ' $x$ ',
we get
$$
\begin{aligned}
2+2\left(y^{\prime \prime}\left(y-y_1\right)+\left(y^{\prime}\right)^2\right] & =0 \\
\Rightarrow \quad\left(y-y_1\right) & =\frac{1-\left(y^{\prime}\right)^2}{y^{\prime \prime}}
\end{aligned}
$$
Sub. values in Eq. (i)
$$
\begin{aligned}
=\left[\frac{1+\left(y^{\prime}\right)^2}{y^{\prime \prime}} \cdot y^{\prime}\right\rceil^2+\left[\frac{1+\left(y^{\prime}\right)^2}{y^{\prime \prime}}\right] & =25 \\
\Rightarrow \quad \frac{\left(1+y^{\prime 2}\right)}{\left(y^{\prime \prime}\right)^2} \cdot\left(y^{\prime}\right)^2+\frac{1+\left(y^{\prime}\right)^2}{\left(y^{\prime \prime}\right)^2} & =25 \\
\Rightarrow \quad \frac{\left(1+y^{\prime}\right)^3}{\left(y^{\prime \prime}\right)^2} & =25 \\
\Rightarrow 25\left(y^{\prime \prime}\right)^2=\left[1+\left(y^{\prime}\right)^2\right]^3 &
\end{aligned}
$$
So, order $=2$ and degree $=2$
$$
\begin{aligned}
& \therefore \quad l=2 \text { and } m=2 \\
& \text { Now, } \quad 2 l+3 m=2 \times 2+3 \times 2 \\
& =4+6=10 \\
&
\end{aligned}
$$
$$
\left(x-x_1\right)^2+\left(y-y_1\right)^2=5^2
$$

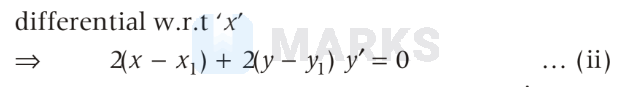
$$
\Rightarrow \quad\left(x-x_1\right)=-\left(y-y_1\right) y^{\prime}
$$
Now Eq. (ii) diff again w.r.t ' $x$ ',
we get
$$
\begin{aligned}
2+2\left(y^{\prime \prime}\left(y-y_1\right)+\left(y^{\prime}\right)^2\right] & =0 \\
\Rightarrow \quad\left(y-y_1\right) & =\frac{1-\left(y^{\prime}\right)^2}{y^{\prime \prime}}
\end{aligned}
$$
Sub. values in Eq. (i)
$$
\begin{aligned}
=\left[\frac{1+\left(y^{\prime}\right)^2}{y^{\prime \prime}} \cdot y^{\prime}\right\rceil^2+\left[\frac{1+\left(y^{\prime}\right)^2}{y^{\prime \prime}}\right] & =25 \\
\Rightarrow \quad \frac{\left(1+y^{\prime 2}\right)}{\left(y^{\prime \prime}\right)^2} \cdot\left(y^{\prime}\right)^2+\frac{1+\left(y^{\prime}\right)^2}{\left(y^{\prime \prime}\right)^2} & =25 \\
\Rightarrow \quad \frac{\left(1+y^{\prime}\right)^3}{\left(y^{\prime \prime}\right)^2} & =25 \\
\Rightarrow 25\left(y^{\prime \prime}\right)^2=\left[1+\left(y^{\prime}\right)^2\right]^3 &
\end{aligned}
$$
So, order $=2$ and degree $=2$
$$
\begin{aligned}
& \therefore \quad l=2 \text { and } m=2 \\
& \text { Now, } \quad 2 l+3 m=2 \times 2+3 \times 2 \\
& =4+6=10 \\
&
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.