Search any question & find its solution
Question:
Answered & Verified by Expert
If light passes near a massive object, the gravitational interaction causes a bending of the ray. This can be thought of as happening due to a change in the effective refractive index of the medium given by
$$
\mathrm{n}(\mathrm{r})=1+2 \mathrm{GM} / \mathrm{rc}^2
$$
where $r$ is the distance of the point of consideration from the centre of the mass of the massive body, $G$ is the universal gravitational constant, $M$ the mass of the body and $c$ the speed of light in vacuum. Considering a spherical object find the deviation of the ray from the original path as it grazes the object.
$$
\mathrm{n}(\mathrm{r})=1+2 \mathrm{GM} / \mathrm{rc}^2
$$
where $r$ is the distance of the point of consideration from the centre of the mass of the massive body, $G$ is the universal gravitational constant, $M$ the mass of the body and $c$ the speed of light in vacuum. Considering a spherical object find the deviation of the ray from the original path as it grazes the object.
Solution:
2564 Upvotes
Verified Answer
Consider two planes $A$ and $B$ at $r$ and $(r+d r)$ distance from the center of massive object of mass $\mathrm{M}$ and let the ray be incident at an angle $\theta$ at the plane at $r$ and leave $r+d r$ at an angle $\theta+d \theta$.
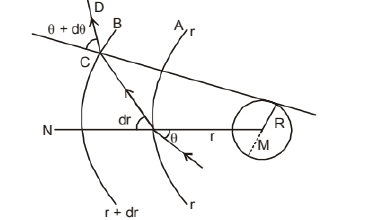
By Snell's law,
$$
\begin{aligned}
&n(r) \sin \theta \cong n(r+d r) \sin (\theta+d \theta) \\
&n(r) \sin \theta \cong\left(n(r)+\frac{d n}{d r} d r\right) \times(\sin \theta \cos d \theta+\cos \theta \sin d \theta)
\end{aligned}
$$
$$
\begin{aligned}
\mathrm{n}(\mathrm{r}) \sin \theta \cong &\left(\mathrm{n}(\mathrm{r})+\frac{\mathrm{dn}}{\mathrm{dr}} \mathrm{dr}\right)(\sin \theta+\cos \theta \mathrm{d} \theta) \\
& {[\because \mathrm{d} \theta \rightarrow 0 \text { then } \cos \mathrm{d} \theta=1 \text { and }(\sin \mathrm{d} \theta=\mathrm{d} \theta)] }
\end{aligned}
$$
Ignoring the product of differentials
$$
\begin{aligned}
&\mathrm{n}(\mathrm{r}) \sin \theta=\mathrm{n}(\mathrm{r}) \sin \theta+\mathrm{r} \sin \theta\left(\frac{\mathrm{dn}}{\mathrm{dr}}\right) \\
&+\mathrm{n}(\mathrm{r}) \cos \theta\left(\frac{\mathrm{d} \theta}{\mathrm{dr}}\right)+\left(\frac{\mathrm{dr}}{\mathrm{dr}}\right) \cos \theta(\mathrm{d} \theta) \\
&\text { or, } \quad-\frac{\mathrm{dn}}{\mathrm{dr}} \tan \theta=\mathrm{n}(\mathrm{r}) \frac{\mathrm{d} \theta}{\mathrm{dr}}\left[\because \operatorname{given} \mathrm{n}(\mathrm{r})=1+\frac{2 \mathrm{GM}}{\mathrm{rc}^2}\right] \\
&\frac{2 \mathrm{GM}}{\mathrm{r}^2 \mathrm{c}^2} \tan \theta=\left(1+\frac{2 \mathrm{GM}}{\mathrm{rc}^2}\right) \frac{\mathrm{d} \theta}{\mathrm{dr}} \approx \frac{\mathrm{d} \theta}{\mathrm{dr}}
\end{aligned}
$$
As the $\mathrm{G}$ is very small and $\mathrm{c}^2$ is very large
$$
\begin{aligned}
&\text { So, } \quad \frac{2 \mathrm{GM}}{\mathrm{rc}^2} \rightarrow 0 \\
&\frac{2 \mathrm{GM}}{\mathrm{r}^2 \mathrm{c}^2} \tan \theta=\frac{\mathrm{d} \theta}{\mathrm{dr}}
\end{aligned}
$$
intigrating both sides,
$$
\int_0^{\theta_0} d \theta=\frac{2 G M}{c^2} \int_{-\infty}^{\infty} \frac{\tan \theta d r}{r^2}
$$
Now substitution for integrals, we get
$$
\begin{aligned}
&\mathrm{r}^2=\mathrm{x}^2+\mathrm{R}^2 \text { and } \tan \theta=\frac{\mathrm{R}}{\mathrm{x}} \\
&\int_0^{\theta_0} \mathrm{~d} \theta=\frac{2 \mathrm{GM}}{\mathrm{c}^2} \int_{-\infty}^{\infty} \frac{1}{\mathrm{r}^2} \frac{\mathrm{R}}{\mathrm{r}} \mathrm{dx}=\frac{2 \mathrm{GM}}{\mathrm{c}^2} \int_{-\infty}^{\infty} \frac{\mathrm{Rx}}{\mathrm{xr}^3} \mathrm{dx} \\
&\int_0^{\theta_0} \mathrm{~d} \theta=\frac{2 \mathrm{GM}}{\mathrm{c}^2} \int_{-\infty}^{\infty} \frac{\mathrm{R}}{\mathrm{x}} \frac{\mathrm{xdx}}{\left(\mathrm{x}^2+\mathrm{R}^2\right)^{3 / 2}} \\
&\mathrm{x}=\mathrm{R} \tan \phi \text { (putting) } \\
&\mathrm{dx}=\mathrm{R} \sec ^2 \phi \mathrm{d} \phi \\
&\mathrm{q}_0=\frac{2 \mathrm{GMR}}{\mathrm{c}^2} \int_{-\pi / 2}^{\pi / 2} \frac{\mathrm{R} \sec ^2 \phi \mathrm{d} \phi}{\mathrm{R}^3 \sec ^3 \phi}=\frac{2 \mathrm{GM}}{\mathrm{Rc}^2} \int_{-\pi / 2}^{\pi / 2} \cos \phi \mathrm{d} \phi=\frac{4 \mathrm{Gm}}{\mathrm{Rc}^2} \\
&\text { or, } \quad \theta_0=\frac{4 \mathrm{GM}}{\mathrm{Rc}^2}
\end{aligned}
$$

By Snell's law,
$$
\begin{aligned}
&n(r) \sin \theta \cong n(r+d r) \sin (\theta+d \theta) \\
&n(r) \sin \theta \cong\left(n(r)+\frac{d n}{d r} d r\right) \times(\sin \theta \cos d \theta+\cos \theta \sin d \theta)
\end{aligned}
$$
$$
\begin{aligned}
\mathrm{n}(\mathrm{r}) \sin \theta \cong &\left(\mathrm{n}(\mathrm{r})+\frac{\mathrm{dn}}{\mathrm{dr}} \mathrm{dr}\right)(\sin \theta+\cos \theta \mathrm{d} \theta) \\
& {[\because \mathrm{d} \theta \rightarrow 0 \text { then } \cos \mathrm{d} \theta=1 \text { and }(\sin \mathrm{d} \theta=\mathrm{d} \theta)] }
\end{aligned}
$$
Ignoring the product of differentials
$$
\begin{aligned}
&\mathrm{n}(\mathrm{r}) \sin \theta=\mathrm{n}(\mathrm{r}) \sin \theta+\mathrm{r} \sin \theta\left(\frac{\mathrm{dn}}{\mathrm{dr}}\right) \\
&+\mathrm{n}(\mathrm{r}) \cos \theta\left(\frac{\mathrm{d} \theta}{\mathrm{dr}}\right)+\left(\frac{\mathrm{dr}}{\mathrm{dr}}\right) \cos \theta(\mathrm{d} \theta) \\
&\text { or, } \quad-\frac{\mathrm{dn}}{\mathrm{dr}} \tan \theta=\mathrm{n}(\mathrm{r}) \frac{\mathrm{d} \theta}{\mathrm{dr}}\left[\because \operatorname{given} \mathrm{n}(\mathrm{r})=1+\frac{2 \mathrm{GM}}{\mathrm{rc}^2}\right] \\
&\frac{2 \mathrm{GM}}{\mathrm{r}^2 \mathrm{c}^2} \tan \theta=\left(1+\frac{2 \mathrm{GM}}{\mathrm{rc}^2}\right) \frac{\mathrm{d} \theta}{\mathrm{dr}} \approx \frac{\mathrm{d} \theta}{\mathrm{dr}}
\end{aligned}
$$
As the $\mathrm{G}$ is very small and $\mathrm{c}^2$ is very large
$$
\begin{aligned}
&\text { So, } \quad \frac{2 \mathrm{GM}}{\mathrm{rc}^2} \rightarrow 0 \\
&\frac{2 \mathrm{GM}}{\mathrm{r}^2 \mathrm{c}^2} \tan \theta=\frac{\mathrm{d} \theta}{\mathrm{dr}}
\end{aligned}
$$
intigrating both sides,
$$
\int_0^{\theta_0} d \theta=\frac{2 G M}{c^2} \int_{-\infty}^{\infty} \frac{\tan \theta d r}{r^2}
$$
Now substitution for integrals, we get
$$
\begin{aligned}
&\mathrm{r}^2=\mathrm{x}^2+\mathrm{R}^2 \text { and } \tan \theta=\frac{\mathrm{R}}{\mathrm{x}} \\
&\int_0^{\theta_0} \mathrm{~d} \theta=\frac{2 \mathrm{GM}}{\mathrm{c}^2} \int_{-\infty}^{\infty} \frac{1}{\mathrm{r}^2} \frac{\mathrm{R}}{\mathrm{r}} \mathrm{dx}=\frac{2 \mathrm{GM}}{\mathrm{c}^2} \int_{-\infty}^{\infty} \frac{\mathrm{Rx}}{\mathrm{xr}^3} \mathrm{dx} \\
&\int_0^{\theta_0} \mathrm{~d} \theta=\frac{2 \mathrm{GM}}{\mathrm{c}^2} \int_{-\infty}^{\infty} \frac{\mathrm{R}}{\mathrm{x}} \frac{\mathrm{xdx}}{\left(\mathrm{x}^2+\mathrm{R}^2\right)^{3 / 2}} \\
&\mathrm{x}=\mathrm{R} \tan \phi \text { (putting) } \\
&\mathrm{dx}=\mathrm{R} \sec ^2 \phi \mathrm{d} \phi \\
&\mathrm{q}_0=\frac{2 \mathrm{GMR}}{\mathrm{c}^2} \int_{-\pi / 2}^{\pi / 2} \frac{\mathrm{R} \sec ^2 \phi \mathrm{d} \phi}{\mathrm{R}^3 \sec ^3 \phi}=\frac{2 \mathrm{GM}}{\mathrm{Rc}^2} \int_{-\pi / 2}^{\pi / 2} \cos \phi \mathrm{d} \phi=\frac{4 \mathrm{Gm}}{\mathrm{Rc}^2} \\
&\text { or, } \quad \theta_0=\frac{4 \mathrm{GM}}{\mathrm{Rc}^2}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.