\(\begin{aligned}
|z-4+3 i| & \leq 1 \\
|Z-(4-3 i)| & \leq 1
\end{aligned}\)


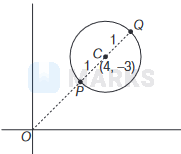
It represent a circle of radius less than or equal to 1 unit
Minimum value of \(|z|=O P=O C-C P=5-1\)
\(m=4\)
Maximum value of \(|z|=O Q=O C+C Q=5+1\)
\(\begin{aligned}
n & =6 \\
\frac{x^4+x^2+4}{x} & =x^3+x+\frac{4}{x} \\
\frac{x^4+x^2+4}{x} & =x^3+x+\frac{1}{x}+\frac{1}{x}+\frac{1}{x}+\frac{1}{x}
\end{aligned}\)
Since, \(\mathrm{AM} \geq \mathrm{GM}\)
\(\begin{aligned}
\frac{x^3+x+\frac{1}{x}+\frac{1}{x}+\frac{1}{x}+\frac{1}{x}}{6} & \geq \sqrt[6]{x^3 \cdot x \cdot \frac{1}{x} \cdot \frac{1}{x} \cdot \frac{1}{x} \cdot \frac{1}{x}} \geq \sqrt[6]{1} \\
x^3+x+\frac{1}{x}+\frac{1}{x}+\frac{1}{x}+\frac{1}{x} & \geq 6 \\
\frac{x^4+x^2+4 x}{4} & \geq 6
\end{aligned}\)
\(\therefore\) Minimum Value of \(\frac{x^4+x^2+x}{4}=6\)
\(\begin{array}{rr}
k=6 & \text { [given] } \\
k=n & {[\because 6=n]}
\end{array}\)
Hence, option (a) is correct.