Search any question & find its solution
Question:
Answered & Verified by Expert
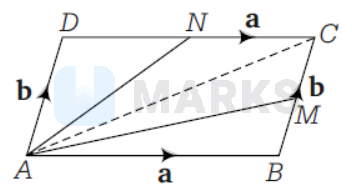
If $M$ and $N$ are the mid-points of the sides $B C$ and $C D$ respectively of a parallelogram $A B C D$, then $\mathbf{A M}+\mathbf{A N}$ equals
Options:
Solution:
2844 Upvotes
Verified Answer
The correct answer is:
$\frac{3}{2} \mathrm{AC}$
$\text {Since, } M \text { and } N \text { are the mid-points of } B C \text { and } C D \text {. }$
$\begin{aligned}
& \therefore & B M & =\frac{1}{2} \mathbf{b} \\
& \text {and } & D N & =\frac{1}{2} \mathbf{a}
\end{aligned}$
Now, in $\triangle A B M$,
$\begin{aligned}
A M & =A B+B M \\
& =\mathbf{a}+\frac{1}{2} \mathbf{b}
\end{aligned}$
and in $\triangle A D N$,
$\begin{aligned}
A N & =A D+D N \\
& =\mathbf{b}+\frac{1}{2} \mathbf{a} \\
\therefore \quad \mathrm{AM}+\mathrm{AN} & =\mathbf{a}+\frac{1}{2} \mathbf{b}+\mathbf{b}+\frac{1}{2} \mathbf{a} \\
& =\frac{3}{2} \mathbf{a}+\frac{3}{2} \mathbf{b}=\frac{3}{2}(\mathbf{a}+\mathbf{b}) \\
\Rightarrow \quad \mathrm{AM}+\mathrm{AN} & =\frac{3}{2} \mathrm{AC} \quad[\because \mathrm{AC}=\mathbf{a}+\mathbf{b}]
\end{aligned}$
$\begin{aligned}
& \therefore & B M & =\frac{1}{2} \mathbf{b} \\
& \text {and } & D N & =\frac{1}{2} \mathbf{a}
\end{aligned}$
Now, in $\triangle A B M$,

$\begin{aligned}
A M & =A B+B M \\
& =\mathbf{a}+\frac{1}{2} \mathbf{b}
\end{aligned}$
and in $\triangle A D N$,
$\begin{aligned}
A N & =A D+D N \\
& =\mathbf{b}+\frac{1}{2} \mathbf{a} \\
\therefore \quad \mathrm{AM}+\mathrm{AN} & =\mathbf{a}+\frac{1}{2} \mathbf{b}+\mathbf{b}+\frac{1}{2} \mathbf{a} \\
& =\frac{3}{2} \mathbf{a}+\frac{3}{2} \mathbf{b}=\frac{3}{2}(\mathbf{a}+\mathbf{b}) \\
\Rightarrow \quad \mathrm{AM}+\mathrm{AN} & =\frac{3}{2} \mathrm{AC} \quad[\because \mathrm{AC}=\mathbf{a}+\mathbf{b}]
\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.