Search any question & find its solution
Question:
Answered & Verified by Expert
If rectangles are inscribed in a circle of radius r units. Then the dimensions of the rectangle which has maximum area are
Options:
Solution:
1095 Upvotes
Verified Answer
The correct answer is:
$\sqrt{2} \mathrm{r}$ units,$\sqrt{2} \mathrm{r}$ units
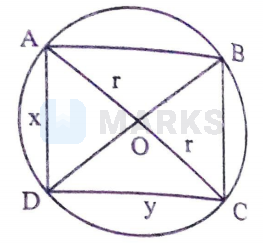
Let $A B C D$ be the rectangle inscribed in a circle of radius 'r'.
$\Rightarrow \mathrm{AC}=\mathrm{BD}=2 \mathrm{r}=$ diameter
Let $x$ and $y$ be the length and breath of rectangle.
$\therefore x^{2}+y^{2}=(2 r)^{2} \Rightarrow y=\sqrt{4 r^{2}-x^{2}}$
Now Area of rectangle $=\mathrm{A}=\mathrm{xy}$
$$
\begin{aligned}
\therefore & A=x \sqrt{4 r^{2}-x^{2}} \\
\therefore & \frac{d A}{d x}=\sqrt{4 r^{2}-x^{2}}+\frac{x}{2 \sqrt{4 r^{2}-x^{2}}} \times(-2 x)=\sqrt{4 r^{2}-x^{2}}-\frac{x^{2}}{\sqrt{4 r^{2}-x^{2}}} \\
& \frac{d A}{d x}=\frac{4 r^{2}-2 x^{2}}{\sqrt{4 r^{2}-x^{2}}}
\end{aligned}
$$
For maximum Area, $\frac{\mathrm{dA}}{\mathrm{dx}}=0 \Rightarrow 4 \mathrm{r}^{2}-2 \mathrm{x}^{2}=0 \Rightarrow \mathrm{x}=\sqrt{2} \mathrm{r}$
$$
\frac{\mathrm{d}^{2} \mathrm{~A}}{\mathrm{dx}^{2}}>0 \text { for } \mathrm{x}=\sqrt{2} \mathrm{r}
$$
Therefore area is maximum when $x=\sqrt{2} r \Rightarrow y=\sqrt{4 r^{2}-2 r^{2}}=\sqrt{2} r$
$\Rightarrow \mathrm{AC}=\mathrm{BD}=2 \mathrm{r}=$ diameter
Let $x$ and $y$ be the length and breath of rectangle.
$\therefore x^{2}+y^{2}=(2 r)^{2} \Rightarrow y=\sqrt{4 r^{2}-x^{2}}$
Now Area of rectangle $=\mathrm{A}=\mathrm{xy}$
$$
\begin{aligned}
\therefore & A=x \sqrt{4 r^{2}-x^{2}} \\
\therefore & \frac{d A}{d x}=\sqrt{4 r^{2}-x^{2}}+\frac{x}{2 \sqrt{4 r^{2}-x^{2}}} \times(-2 x)=\sqrt{4 r^{2}-x^{2}}-\frac{x^{2}}{\sqrt{4 r^{2}-x^{2}}} \\
& \frac{d A}{d x}=\frac{4 r^{2}-2 x^{2}}{\sqrt{4 r^{2}-x^{2}}}
\end{aligned}
$$
For maximum Area, $\frac{\mathrm{dA}}{\mathrm{dx}}=0 \Rightarrow 4 \mathrm{r}^{2}-2 \mathrm{x}^{2}=0 \Rightarrow \mathrm{x}=\sqrt{2} \mathrm{r}$
$$
\frac{\mathrm{d}^{2} \mathrm{~A}}{\mathrm{dx}^{2}}>0 \text { for } \mathrm{x}=\sqrt{2} \mathrm{r}
$$
Therefore area is maximum when $x=\sqrt{2} r \Rightarrow y=\sqrt{4 r^{2}-2 r^{2}}=\sqrt{2} r$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.