Search any question & find its solution
Question:
Answered & Verified by Expert
If $\mathrm{S}$ is the circumcentre, $\mathrm{O}$ is the orthocentre and $\mathrm{G}$ is the centroid of a triangle $\mathrm{ABC}$, then match the items of the List -I with those of the items of List-II given below.

Options:

Solution:
2902 Upvotes
Verified Answer
The correct answer is:
i $\rightarrow$ D, ii $\rightarrow$ C, iii $\rightarrow$ A, iv $\rightarrow$ B
$\mathrm{SA}=\vec{a}, \overrightarrow{\mathrm{SB}}=b, \overrightarrow{\mathrm{SC}}=c$
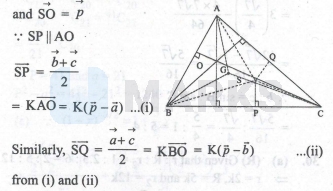
$\begin{aligned} & \vec{p}=\frac{\vec{b}+\vec{c}}{2 k}+\vec{a}=\frac{\vec{a}+\vec{c}}{2 k}+\vec{b} \\ & =\vec{a}+\left(\frac{1}{2 k}\right) \vec{b}+\left(\frac{1}{2 k}\right) \vec{c} \\ & =\left(\frac{1}{2 k}\right) \vec{a}+\left(\frac{1}{2 k}\right) \vec{b}\end{aligned}$
Comparing coefficients
$k=\frac{1}{2}$
$\Rightarrow \vec{p}=\vec{a}+\frac{\vec{b}+\vec{c}}{2\left(\frac{1}{2}\right)}=\vec{a}+\vec{b}+\vec{c}$
$\therefore \overrightarrow{\mathrm{SA}}+\overrightarrow{\mathrm{SB}}+\overrightarrow{\mathrm{SC}}=\overrightarrow{\mathrm{SO}}$
(i) $\rightarrow$ (D)
also we know that centroid divides orthocentre & circumcentre in $2: 1$

$\therefore \overrightarrow{\mathrm{OG}}=\frac{2}{3} \overrightarrow{\mathrm{OS}}$
(iv) $\rightarrow$ (B)
only such option is
(i) $\rightarrow D$, (ii) $\rightarrow C$, (iii) $\rightarrow A$, (iv) $\rightarrow B$

$\begin{aligned} & \vec{p}=\frac{\vec{b}+\vec{c}}{2 k}+\vec{a}=\frac{\vec{a}+\vec{c}}{2 k}+\vec{b} \\ & =\vec{a}+\left(\frac{1}{2 k}\right) \vec{b}+\left(\frac{1}{2 k}\right) \vec{c} \\ & =\left(\frac{1}{2 k}\right) \vec{a}+\left(\frac{1}{2 k}\right) \vec{b}\end{aligned}$
Comparing coefficients
$k=\frac{1}{2}$
$\Rightarrow \vec{p}=\vec{a}+\frac{\vec{b}+\vec{c}}{2\left(\frac{1}{2}\right)}=\vec{a}+\vec{b}+\vec{c}$
$\therefore \overrightarrow{\mathrm{SA}}+\overrightarrow{\mathrm{SB}}+\overrightarrow{\mathrm{SC}}=\overrightarrow{\mathrm{SO}}$
(i) $\rightarrow$ (D)
also we know that centroid divides orthocentre & circumcentre in $2: 1$

$\therefore \overrightarrow{\mathrm{OG}}=\frac{2}{3} \overrightarrow{\mathrm{OS}}$
(iv) $\rightarrow$ (B)
only such option is
(i) $\rightarrow D$, (ii) $\rightarrow C$, (iii) $\rightarrow A$, (iv) $\rightarrow B$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.