If $\sin \left(\cot ^{-1}(1+\mathrm{x})\right)=\cos \left(\tan ^{-1} \mathrm{x}\right)$, then $\mathrm{x}=$

Question

If $\sin \left(\cot ^{-1}(1+\mathrm{x})\right)=\cos \left(\tan ^{-1} \mathrm{x}\right)$, then $\mathrm{x}=$, $\frac{1}{2}$, 1, 0, $-\frac{1}{2}$

MARKS App · Accepted Answer

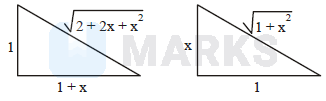
$\begin{aligned} & \sin \left(\cot ^{-1}(1+x)\right)=\frac{1}{\sqrt{2+2 x+x^2}} \ & \cos \left(\tan ^{-1} x\right)=\frac{1}{\sqrt{1+x^2}} \end{aligned}$ So, $\frac{1}{\sqrt{2+2 x+x^2}}=\frac{1}{\sqrt{1+x^2}}$ $\Rightarrow 1+2 \mathrm{x}=0 \Rightarrow \mathrm{x}=-\frac{1}{2}$

Search any question & find its solution

Looking for more such questions to practice?