$\begin{aligned} & \text {} \because \mathrm{x}^2+\mathrm{y}^2-4 \mathrm{x}-8 \mathrm{y}+4=0 \\ & C \equiv \mathrm{x}^2+\mathrm{y}^2\left(-\mathrm{g}_1-\mathrm{f}\right)=(2,4) \mathrm{r}=\sqrt{4+16-4}=4\end{aligned}$



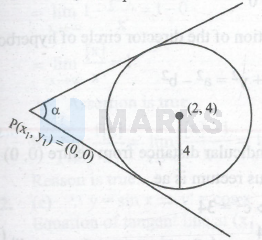
Equation of pair of tangents is $\mathrm{S} \mathrm{S}_1=\mathrm{T}^2$
Where : $S$ : Equation of circle $S_1=S(0,0)$
$$
\begin{aligned}
& \& \mathrm{~T}=\mathrm{xx}_1+\mathrm{y}_1+\mathrm{g}\left(\mathrm{x}+\mathrm{x}_1\right)+\mathrm{f}\left(\mathrm{y}+\mathrm{y}_1\right)+\mathrm{c}=0 \\
& \Rightarrow\left(\mathrm{x}^2+\mathrm{y}^2-4 \mathrm{x}-8 \mathrm{y}+4\right)(0+4)=(\mathrm{x} \cdot 0+\mathrm{y} \cdot 0-2(\mathrm{x}-0) \\
& -4(\mathrm{y}-0)+4)^2 \\
& \Rightarrow 4\left(\mathrm{x}^2+\mathrm{y}^2-4 \mathrm{x}-8 \mathrm{y}+4\right)=(-2 \mathrm{x}-4 \mathrm{y}+4)^2 \\
& \Rightarrow 12 \mathrm{y}^2+16 \mathrm{xy}=0
\end{aligned}
$$
Tangent of acute angle between pairs of straight line $a x^2+2 b x y+b y^2$ is
$$
\tan \alpha=\frac{2\left(h^2-a b\right)}{a+b}
$$
In equation (i) $a=0, b=12, h=8$
$$
\therefore \tan \alpha=\frac{2\left(8^2-0\right)}{12}=\frac{4}{3}
$$