Search any question & find its solution
Question:
Answered & Verified by Expert
If the angle $\theta$ between the vectors $\overrightarrow{\mathbf{a}}=2 x^2 \hat{\mathbf{i}}+4 x \hat{\mathbf{j}}+\hat{\mathbf{k}}$ and $\overrightarrow{\mathbf{b}}=7 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}+x \hat{\mathbf{k}}$ is such that $90^{\circ} < \theta < 180^{\circ}$, then $x$ lies in the interval
Options:
Solution:
2914 Upvotes
Verified Answer
The correct answer is:
$\left(0, \frac{1}{2}\right)$
Given, $\overrightarrow{\mathbf{a}}=2 x^2 \hat{\mathbf{i}}+4 x \hat{\mathbf{j}}+\hat{\mathbf{k}}$
$\overrightarrow{\mathbf{b}}=7 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}+x \hat{\mathbf{k}}$, also $90^{\circ} < \theta < 180^{\circ}$
We know that,
$\cos \theta=\frac{\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}}{|\overrightarrow{\mathbf{a}}||\overrightarrow{\mathbf{b}}|}$
$\cos \theta=\frac{\left(2 x^2 \hat{\mathbf{i}}+4 x \hat{\mathbf{j}}+\hat{\mathbf{k}}\right) \cdot(7 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}+x \hat{\mathbf{k}})}{\sqrt{4 x^4+16 x^2+1} \cdot \sqrt{49+4+x^2}}$
$\cos \theta=\frac{14 x^2-8 x+x}{\sqrt{4 x^4+16 x^2+1} \cdot \sqrt{53+x^2}}$
$=\frac{14 x^2-7 x}{\sqrt{4 x^4+16 x^2+1} \cdot \sqrt{53+x^2}}$
$\cos \theta=\frac{7 x(2 x-1)}{\sqrt{4 x^4+16 x^2+1} \cdot \sqrt{53+x^2}}$
$\because \theta$ lies between $\left(90^{\circ}, 180^{\circ}\right)$
ie, $\cos \theta$ is negative in Ind quadrant.
So, RHS is also negative ie,
$\frac{7 x(2 x-1)}{\sqrt{4 x^4+16 x^2+1} \cdot \sqrt{53+x^2}} < 0$
$7 x(2 x-1) < 0$
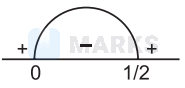
So, $\quad x \in\left(0, \frac{1}{2}\right)$
$\overrightarrow{\mathbf{b}}=7 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}+x \hat{\mathbf{k}}$, also $90^{\circ} < \theta < 180^{\circ}$
We know that,
$\cos \theta=\frac{\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}}{|\overrightarrow{\mathbf{a}}||\overrightarrow{\mathbf{b}}|}$
$\cos \theta=\frac{\left(2 x^2 \hat{\mathbf{i}}+4 x \hat{\mathbf{j}}+\hat{\mathbf{k}}\right) \cdot(7 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}+x \hat{\mathbf{k}})}{\sqrt{4 x^4+16 x^2+1} \cdot \sqrt{49+4+x^2}}$
$\cos \theta=\frac{14 x^2-8 x+x}{\sqrt{4 x^4+16 x^2+1} \cdot \sqrt{53+x^2}}$
$=\frac{14 x^2-7 x}{\sqrt{4 x^4+16 x^2+1} \cdot \sqrt{53+x^2}}$
$\cos \theta=\frac{7 x(2 x-1)}{\sqrt{4 x^4+16 x^2+1} \cdot \sqrt{53+x^2}}$
$\because \theta$ lies between $\left(90^{\circ}, 180^{\circ}\right)$
ie, $\cos \theta$ is negative in Ind quadrant.
So, RHS is also negative ie,
$\frac{7 x(2 x-1)}{\sqrt{4 x^4+16 x^2+1} \cdot \sqrt{53+x^2}} < 0$
$7 x(2 x-1) < 0$

So, $\quad x \in\left(0, \frac{1}{2}\right)$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.