Search any question & find its solution
Question:
Answered & Verified by Expert
If the first line in the Lyman series has wavelength $\lambda$, then the first line in Balmer series has the wavelength
Options:
Solution:
2111 Upvotes
Verified Answer
The correct answer is:
$\frac{27}{5} \lambda$
Wavelength for Lyman series is calculated as
$\frac{1}{\lambda}=R\left(\frac{1}{1^2}-\frac{1}{n^2}\right)$
For first line of Lyman series, $n=2$
$\therefore \quad \frac{1}{\lambda}=R\left(\frac{1}{1^2}-\frac{1}{2^2}\right) \Rightarrow \frac{1}{\lambda}=\frac{3 R}{4}$
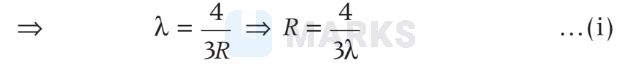
Wavelength of Balmer series is calculated as
$\frac{1}{\lambda^{\prime}}=R\left(\frac{1}{2^2}-\frac{1}{n^2}\right)$
For first line of Balmer series, $n=3$
$\begin{array}{ll}\therefore & \frac{1}{\lambda^{\prime}}=R\left(\frac{1}{2^2}-\frac{1}{3^2}\right) \\ \Rightarrow & \frac{1}{\lambda^{\prime}}=\frac{5}{36} R \Rightarrow \frac{1}{\lambda^{\prime}}=\frac{5}{36} \times \frac{4}{3 \lambda} \quad \text { [from Eq. (i)] } \\ \Rightarrow & \frac{1}{\lambda^{\prime}}=\frac{5}{27 \lambda} \Rightarrow \lambda^{\prime}=\frac{27 \lambda}{5}\end{array}$
$\frac{1}{\lambda}=R\left(\frac{1}{1^2}-\frac{1}{n^2}\right)$
For first line of Lyman series, $n=2$
$\therefore \quad \frac{1}{\lambda}=R\left(\frac{1}{1^2}-\frac{1}{2^2}\right) \Rightarrow \frac{1}{\lambda}=\frac{3 R}{4}$
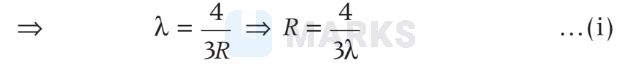
Wavelength of Balmer series is calculated as
$\frac{1}{\lambda^{\prime}}=R\left(\frac{1}{2^2}-\frac{1}{n^2}\right)$
For first line of Balmer series, $n=3$
$\begin{array}{ll}\therefore & \frac{1}{\lambda^{\prime}}=R\left(\frac{1}{2^2}-\frac{1}{3^2}\right) \\ \Rightarrow & \frac{1}{\lambda^{\prime}}=\frac{5}{36} R \Rightarrow \frac{1}{\lambda^{\prime}}=\frac{5}{36} \times \frac{4}{3 \lambda} \quad \text { [from Eq. (i)] } \\ \Rightarrow & \frac{1}{\lambda^{\prime}}=\frac{5}{27 \lambda} \Rightarrow \lambda^{\prime}=\frac{27 \lambda}{5}\end{array}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.