Given, latus rectum of hyperbola subtends 90º at its centre.
Let there be a hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
So, eccentricity, $e=\sqrt{1+\frac{b^2}{a^2}}$
End points of latusrectum are
$$
L=\left(a e, \frac{b^2}{a}\right) \text { and } L^{\prime}=\left(a e, \frac{-b^2}{a}\right)
$$


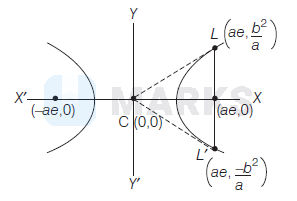
Centre = (0, 0)
$$
\because \quad \angle L C L^{\prime}=90^{\circ}
$$

Then, in $\Delta L C L^{\prime}$, by using Pythagoras theorem,
$$
\begin{aligned}
(L C)^2+\left(L^{\prime} C\right)^2 & =\left(L L^{\prime}\right)^2 \\
(a e-0)^2 & +\left(\frac{b^2}{a}-0\right)^2+(a e-0)^2+\left(\frac{-b^2}{a}-0\right)^2 \\
& =\left(\frac{2 b^2}{a}\right)^2
\end{aligned}
$$
$$
\begin{aligned}
& 2\left(a^2 e^2+\frac{b^4}{a^2}\right)=\frac{4 b^4}{a^2} \Rightarrow \frac{2 b^4}{a^2}=2 a^2 e^2 \\
& \Rightarrow \quad b^4=a^4 e^2 \\
& {\left[a^2\left(e^2-1\right)\right]^2=a^4 e^2 \quad\left\{\because b^2=a^2\left(e^2-1\right)\right\}} \\
& a^4\left(e^2-1\right)^2=a^4 e^2 \\
& \Rightarrow \quad\left(e^2-1\right)^2=e^2 \Rightarrow e^2-1= \pm e \\
& \Rightarrow e^2 \pm e-1=0 \\
& \Rightarrow \quad e=\frac{ \pm 1 \pm \sqrt{1+4}}{2}=\frac{ \pm 1 \pm \sqrt{5}}{2} \\
&
\end{aligned}
$$
$\because e$ can't be negative, hence $e=\frac{\sqrt{5}-1}{2}, \frac{\sqrt{5}+1}{2}$.