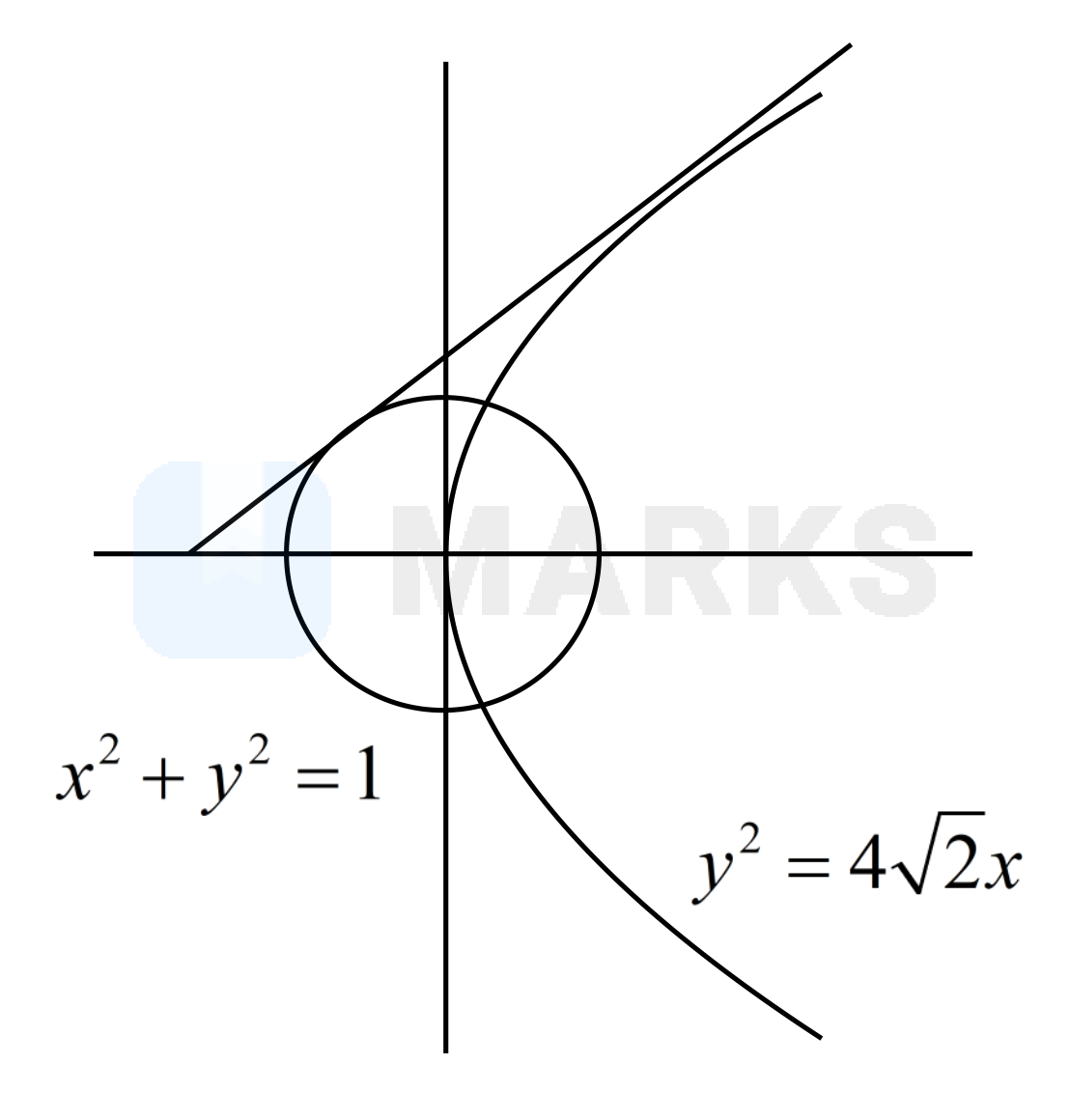
The equation of the tangent to the parabola $y^2=4ax$ is $y=mx+\frac{a}{m}.$

Hence, the equation of tangent to the parabola $y^2=4\sqrt{2}x$ is $y=mx+\frac{\sqrt{2}}{m} ...\left(1\right)$

A line $y=mx+c$ is a tangent to the circle $x^2+y^2=r^2$ if $c^2=r^2\left(1+m^2\right).$

Hence, the line $\left(1\right)$ is also a tangent to the circle $x^2+y^2=1,$ if ${\left(\frac{\sqrt{2}}{m}\right)}^2=1\left(m^2+1\right)$

$\Rightarrow m^2\left(m^2+1\right)-2=0$

$\Rightarrow m^4+m^2-2=0$

$\Rightarrow \left(m^2+2\right)\left(m^2-1\right)=0$

$\Rightarrow m^2=1$ since $m^2+2\ne 0$

$\Rightarrow m=\pm 1.$

Thus, the equation of the common tangent is $y=\pm x\pm \sqrt{2}, \Rightarrow \pm x-y=\mp \sqrt{2}.$

Given, the equation of the common tangent is $ax+y=c$, hence, $c=\pm \sqrt{2}$ and $\left|c\right|=\sqrt{2}.$