Search any question & find its solution
Question:
Answered & Verified by Expert
If the line $x+3 y=0$ is the tangent at $(0,0)$ to the circle of radius 1 , then the centre of one such circle is
Options:
Solution:
1392 Upvotes
Verified Answer
The correct answer is:
$\left(\frac{1}{\sqrt{10}}, \frac{3}{\sqrt{10}}\right)$
Given line is $x+3 y=0$.
$\therefore$ Slope of a line $=-\frac{1}{3}$
Let the centres of circle be $(+g,+f)$.
We know that, the perpendicular drawn from the centre to the tangent is equal to radius.
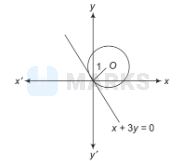
Since perpendicular distance from $(g, f)$ to the line is 1 .
Since perpendicular distance from $(g, f)$ to the line is 1 .
$\begin{array}{ll}\therefore & \frac{+g+3 f}{\sqrt{1^2+3^2}}=1 \\ \Rightarrow & \frac{+g+3 f}{\sqrt{10}}=1\end{array}$
Taking option (d) i.e., centre $=\left(\frac{1}{\sqrt{10}}, \frac{3}{\sqrt{10}}\right)$
$\therefore \quad \frac{+\frac{1}{\sqrt{10}}+3 \times \frac{3}{\sqrt{10}}}{\sqrt{10}}=\frac{10}{10}=1$ (true)
$\therefore$ Slope of a line $=-\frac{1}{3}$
Let the centres of circle be $(+g,+f)$.
We know that, the perpendicular drawn from the centre to the tangent is equal to radius.

Since perpendicular distance from $(g, f)$ to the line is 1 .
Since perpendicular distance from $(g, f)$ to the line is 1 .
$\begin{array}{ll}\therefore & \frac{+g+3 f}{\sqrt{1^2+3^2}}=1 \\ \Rightarrow & \frac{+g+3 f}{\sqrt{10}}=1\end{array}$
Taking option (d) i.e., centre $=\left(\frac{1}{\sqrt{10}}, \frac{3}{\sqrt{10}}\right)$
$\therefore \quad \frac{+\frac{1}{\sqrt{10}}+3 \times \frac{3}{\sqrt{10}}}{\sqrt{10}}=\frac{10}{10}=1$ (true)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.