Search any question & find its solution
Question:
Answered & Verified by Expert
If the point $P(1,3)$ undergoes the following transformations successively.
(i) Reflection with respect to the line $y=x$.
(ii) Translation through 3 units along the positive direction of the $X$-axis.
(iii) Rotation through an angle of $\frac{\pi}{6}$ about the origin in the clockwise direction.
Then, the final position of the point $P$ is
Options:
(i) Reflection with respect to the line $y=x$.
(ii) Translation through 3 units along the positive direction of the $X$-axis.
(iii) Rotation through an angle of $\frac{\pi}{6}$ about the origin in the clockwise direction.
Then, the final position of the point $P$ is
Solution:
1953 Upvotes
Verified Answer
The correct answer is:
$\left(\frac{6 \sqrt{3}+1}{2}, \frac{\sqrt{3}-6}{2}\right)$
The reflection of the point $P(1,3)$ about the line $y=x$ is $Q(3,1)$
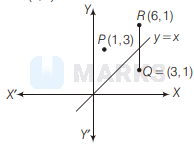
After translation through a distance 3 units along the positive direction of $X$-axis at the point whose coordinate are $R(6,1)$. After rotation through an angle of $\frac{\pi}{6}$ about the origin in the clockwise direction, then $R$ goes to whose coordinates are
$$
R^{\prime}\left(\frac{6 \sqrt{3}+1}{2}, \frac{\sqrt{3}-6}{2}\right)
$$
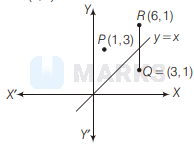
After translation through a distance 3 units along the positive direction of $X$-axis at the point whose coordinate are $R(6,1)$. After rotation through an angle of $\frac{\pi}{6}$ about the origin in the clockwise direction, then $R$ goes to whose coordinates are
$$
R^{\prime}\left(\frac{6 \sqrt{3}+1}{2}, \frac{\sqrt{3}-6}{2}\right)
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.