Search any question & find its solution
Question:
Answered & Verified by Expert
If the points $A(-1,0,7), B(3,2, t), C(5, k,-2)$ are collinear, then the ratio in which the point $P(t, k-2 t, t+k)$ divides the line segment $B C$ is
Options:
Solution:
2480 Upvotes
Verified Answer
The correct answer is:
$-1: 2$
We have, $A(-1,0,7), B(3,2, t)$ and $C(5, k,-2)$ are collinear.
$\therefore \quad \frac{3+1}{5-3}=\frac{2-0}{k-2}=\frac{t-7}{-2-t}$
$\begin{aligned}
& \Rightarrow \quad 2=\frac{2}{k-2}=\frac{t-7}{-2-t} \Rightarrow k=3, t=1 \\
& \therefore \quad B=(3,2,1), C=(5,3,-2) \text { and } P(1,1,4) \\
&
\end{aligned}$
Let $P$ divides $B C$ in the ratio $\lambda: 1$
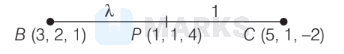
$\begin{aligned} & \therefore \quad \frac{5 \lambda+3}{\lambda+1}=1 \\ & \Rightarrow \quad 5 \lambda+3=\lambda+1 \Rightarrow 4 \lambda=-2 \Rightarrow \lambda=-\frac{1}{2} \\ & \therefore \text { Required ratio }=-1: 2\end{aligned}$
$\therefore \quad \frac{3+1}{5-3}=\frac{2-0}{k-2}=\frac{t-7}{-2-t}$
$\begin{aligned}
& \Rightarrow \quad 2=\frac{2}{k-2}=\frac{t-7}{-2-t} \Rightarrow k=3, t=1 \\
& \therefore \quad B=(3,2,1), C=(5,3,-2) \text { and } P(1,1,4) \\
&
\end{aligned}$
Let $P$ divides $B C$ in the ratio $\lambda: 1$
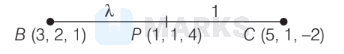
$\begin{aligned} & \therefore \quad \frac{5 \lambda+3}{\lambda+1}=1 \\ & \Rightarrow \quad 5 \lambda+3=\lambda+1 \Rightarrow 4 \lambda=-2 \Rightarrow \lambda=-\frac{1}{2} \\ & \therefore \text { Required ratio }=-1: 2\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.