Search any question & find its solution
Question:
Answered & Verified by Expert
If the roots of the equation $x^3-7 x^2+14 x-8=0$ are in geometric progression, then the difference between the largest and the smallest roots is
Options:
Solution:
1260 Upvotes
Verified Answer
The correct answer is:
3
Given equation, $x^3-7 x^2+14 x-8=0$
Let the roots of this equation are $\frac{a}{r}, a, a r$.
Then, we get
Sum of roots $=7$
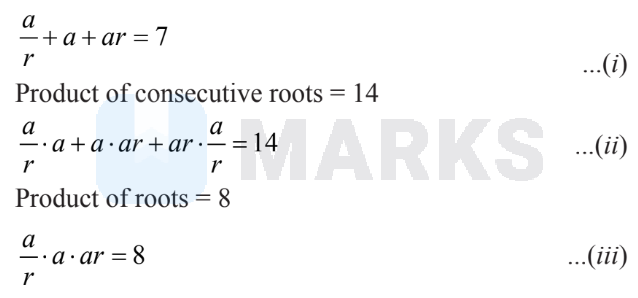
From Eq. (iii), we get $a=2$
Now, from Eq. ( $i)$, we get
$$
\begin{aligned}
& \frac{2}{r}+2 r=5 \\
& \Rightarrow \quad 2+2 r^2=5 r \\
& \Rightarrow \quad 2 r^2-5 r+2=0 \\
& \Rightarrow \quad 2 r^2-4 r-r+2=0 \\
& \Rightarrow \quad 2 r(r-2)-1(r-2)=0 \\
& \Rightarrow \quad(r-2)(2 r-1)=0 \\
& \Rightarrow \quad r=2 \text { or } r=\frac{1}{2}
\end{aligned}
$$
Thus, the roots are 1, 2, 4 .
Hence, difference of largest and smallest number $=4-1=3$
Let the roots of this equation are $\frac{a}{r}, a, a r$.
Then, we get
Sum of roots $=7$
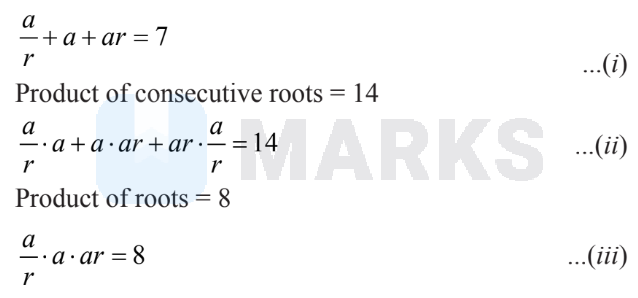
From Eq. (iii), we get $a=2$
Now, from Eq. ( $i)$, we get
$$
\begin{aligned}
& \frac{2}{r}+2 r=5 \\
& \Rightarrow \quad 2+2 r^2=5 r \\
& \Rightarrow \quad 2 r^2-5 r+2=0 \\
& \Rightarrow \quad 2 r^2-4 r-r+2=0 \\
& \Rightarrow \quad 2 r(r-2)-1(r-2)=0 \\
& \Rightarrow \quad(r-2)(2 r-1)=0 \\
& \Rightarrow \quad r=2 \text { or } r=\frac{1}{2}
\end{aligned}
$$
Thus, the roots are 1, 2, 4 .
Hence, difference of largest and smallest number $=4-1=3$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.