Search any question & find its solution
Question:
Answered & Verified by Expert
If two sides of a triangle are given by $3 x^2-5 x y+2 y^2=0$ and its orthocentre is $(2,1)$, then the equation of the third side of the triangle is
Options:
Solution:
2573 Upvotes
Verified Answer
The correct answer is:
$10 x+5 y=21$
Given pair equation of two sides of triangle,
$$
\begin{aligned}
3 x^2-5 x y+2 y^2 & =0 \\
\Rightarrow \quad(3 x-2 y)(x-y) & =0
\end{aligned}
$$
So, equation of sides are
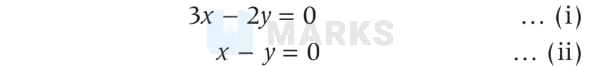
Perpendicular line to the Eq. (i)
$2 x+3 y+k=0$ which pass through the point $(2,1)$.
$$
\Rightarrow \quad 4+3+k=0
$$
$\Rightarrow \quad k=-7$
Point of intersection of Eqs. (ii) and (iii)
$$
x=\frac{7}{5}, y=\frac{7}{5} \Rightarrow\left(\frac{7}{5}, \frac{7}{5}\right)
$$
Perpendicular line to the Eq. (2) is
$$
\begin{array}{ll}
x+y+k=0 \text { which pass through }(2,1) \\
\Rightarrow & 2+1+k=0 \\
\Rightarrow & k=-3
\end{array}
$$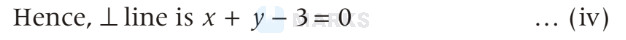
Point of intersection of Eqs. (iv) and (i)
$$
\begin{aligned}
x+y-3 & =0 \\
3 x-2 y & =0 \Rightarrow x=\frac{6}{5}, y=\frac{9}{5} \Rightarrow\left(\frac{6}{5}, \frac{9}{5}\right)
\end{aligned}
$$
So, third side of triangle pass through these point $\left(\frac{7}{5}, \frac{7}{5}\right)$ and $\left(\frac{6}{5}, \frac{9}{5}\right)$ is
$$
\begin{array}{ll}
\Rightarrow & y-\frac{7}{5}=\frac{\frac{9}{5}-\frac{7}{5}}{\frac{6}{5}-\frac{7}{5}}\left(x-\frac{7}{5}\right) \\
\Rightarrow & y-\frac{7}{5}=\frac{2}{-1}\left(x-\frac{7}{5}\right) \\
\Rightarrow & \frac{5 y-7}{5}=\frac{-10 x+14}{5} \\
\Rightarrow & 10 x+5 y=21 .
\end{array}
$$
$$
\begin{aligned}
3 x^2-5 x y+2 y^2 & =0 \\
\Rightarrow \quad(3 x-2 y)(x-y) & =0
\end{aligned}
$$
So, equation of sides are
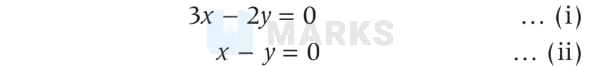
Perpendicular line to the Eq. (i)
$2 x+3 y+k=0$ which pass through the point $(2,1)$.
$$
\Rightarrow \quad 4+3+k=0
$$
$\Rightarrow \quad k=-7$

Point of intersection of Eqs. (ii) and (iii)
$$
x=\frac{7}{5}, y=\frac{7}{5} \Rightarrow\left(\frac{7}{5}, \frac{7}{5}\right)
$$
Perpendicular line to the Eq. (2) is
$$
\begin{array}{ll}
x+y+k=0 \text { which pass through }(2,1) \\
\Rightarrow & 2+1+k=0 \\
\Rightarrow & k=-3
\end{array}
$$
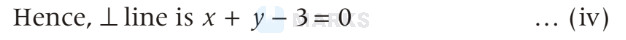
Point of intersection of Eqs. (iv) and (i)
$$
\begin{aligned}
x+y-3 & =0 \\
3 x-2 y & =0 \Rightarrow x=\frac{6}{5}, y=\frac{9}{5} \Rightarrow\left(\frac{6}{5}, \frac{9}{5}\right)
\end{aligned}
$$
So, third side of triangle pass through these point $\left(\frac{7}{5}, \frac{7}{5}\right)$ and $\left(\frac{6}{5}, \frac{9}{5}\right)$ is
$$
\begin{array}{ll}
\Rightarrow & y-\frac{7}{5}=\frac{\frac{9}{5}-\frac{7}{5}}{\frac{6}{5}-\frac{7}{5}}\left(x-\frac{7}{5}\right) \\
\Rightarrow & y-\frac{7}{5}=\frac{2}{-1}\left(x-\frac{7}{5}\right) \\
\Rightarrow & \frac{5 y-7}{5}=\frac{-10 x+14}{5} \\
\Rightarrow & 10 x+5 y=21 .
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.