Search any question & find its solution
Question:
Answered & Verified by Expert
If \(y=\sqrt{3} x+k_1\) and \(y=\sqrt{3} x+k_2\) are two parallel tangents of a circle of radius 2 units, then \(\left|k_1-k_2\right|\) is equal to
Options:
Solution:
2013 Upvotes
Verified Answer
The correct answer is:
8
The distance between parallel tangents to a circle is equals to the diameter of the circle, so
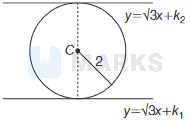
\(\begin{aligned}
& \frac{\left|k_1-k_2\right|}{\sqrt{1+3}}=4 \\
\Rightarrow \quad & \left|k_1-k_2\right|=8
\end{aligned}\)
Hence, option (b) is correct.

\(\begin{aligned}
& \frac{\left|k_1-k_2\right|}{\sqrt{1+3}}=4 \\
\Rightarrow \quad & \left|k_1-k_2\right|=8
\end{aligned}\)
Hence, option (b) is correct.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.