Search any question & find its solution
Question:
Answered & Verified by Expert
$\text { In a } \triangle A B C, \frac{\Delta^2}{a^2+b^2+c^2}\left(\frac{1}{r_1^2}+\frac{1}{r_2^2}+\frac{1}{r_3^2}+\frac{1}{r^2}\right)=$
Options:
Solution:
1263 Upvotes
Verified Answer
The correct answer is:
1
$\frac{\Delta^2}{a^2+b^2+c^2}\left(\frac{1}{r_1^2}+\frac{1}{r_2^2}+\frac{1}{r_3^2}+\frac{1}{r^2}\right)$
$=\frac{\Delta^2}{a^2+b^2+c^2}\left[\frac{(s-a)^2}{\Delta^2}+\frac{(s-b)^2}{\Delta^2}+\frac{(s-c)^2}{\Delta^2}+\frac{s^2}{\Delta^2}\right]$
$=\frac{1}{a^2+b^2+c^2}\left[(s-a)^2+(s-b)^2+(s-c)^2+s^2\right]$
$=\frac{1}{a^2+b^2+c^2}$ $\left[\left(\frac{a+b+c}{2}-a\right)^2+\left(\frac{a+b+c}{2}-b\right)^2\right.$ $\left.+\left(\frac{a+b+c}{2}-c\right)^2+\left(\frac{a+b+c}{2}\right)^2\right]$
$=\frac{1}{a^2+b^2+c^2}$ $\left[\left(\frac{b+c-a}{2}\right)^2+\left(\frac{a+c-b}{2}\right)^2+\left(\frac{a+b-c}{2}\right)^2\right.$ $\left.+\left(\frac{a+b+c}{2}\right)^2\right]$
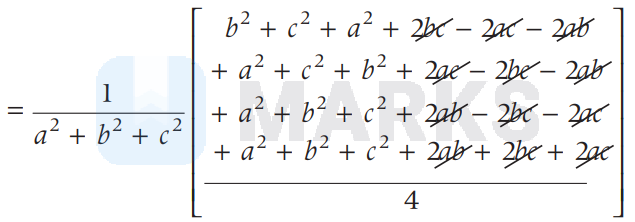
$=\frac{1}{a^2+b^2+c^2}\left[\frac{4\left(a^2+b^2+c^2\right)}{4}\right]=1$
$=\frac{\Delta^2}{a^2+b^2+c^2}\left[\frac{(s-a)^2}{\Delta^2}+\frac{(s-b)^2}{\Delta^2}+\frac{(s-c)^2}{\Delta^2}+\frac{s^2}{\Delta^2}\right]$
$=\frac{1}{a^2+b^2+c^2}\left[(s-a)^2+(s-b)^2+(s-c)^2+s^2\right]$
$=\frac{1}{a^2+b^2+c^2}$ $\left[\left(\frac{a+b+c}{2}-a\right)^2+\left(\frac{a+b+c}{2}-b\right)^2\right.$ $\left.+\left(\frac{a+b+c}{2}-c\right)^2+\left(\frac{a+b+c}{2}\right)^2\right]$
$=\frac{1}{a^2+b^2+c^2}$ $\left[\left(\frac{b+c-a}{2}\right)^2+\left(\frac{a+c-b}{2}\right)^2+\left(\frac{a+b-c}{2}\right)^2\right.$ $\left.+\left(\frac{a+b+c}{2}\right)^2\right]$
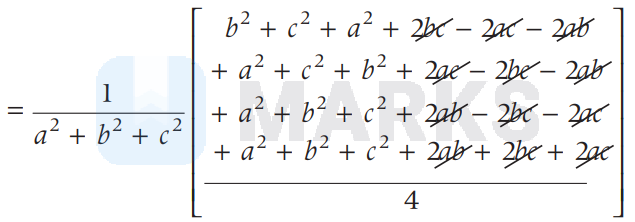
$=\frac{1}{a^2+b^2+c^2}\left[\frac{4\left(a^2+b^2+c^2\right)}{4}\right]=1$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.