Search any question & find its solution
Question:
Answered & Verified by Expert
In a circle with centre $\mathrm{O}$, suppose A, P, B are three points on its circumference such that $\mathrm{P}$ is the mid-point of minor arc $\mathrm{AB}$. Suppose when $\angle \mathrm{AOB}=\theta$,
$\frac{\operatorname{area}(\Delta \mathrm{AOB})}{\text { area }(\Delta \mathrm{APB})}=\sqrt{5}+2$
If $\angle \mathrm{AOB}$ is doubled to $2 \theta$, then the ratio $\frac{\text { area }(\Delta \mathrm{AOB})}{\text { area }(\triangle \mathrm{APB})}$ is -
Options:
$\frac{\operatorname{area}(\Delta \mathrm{AOB})}{\text { area }(\Delta \mathrm{APB})}=\sqrt{5}+2$
If $\angle \mathrm{AOB}$ is doubled to $2 \theta$, then the ratio $\frac{\text { area }(\Delta \mathrm{AOB})}{\text { area }(\triangle \mathrm{APB})}$ is -
Solution:
2332 Upvotes
Verified Answer
The correct answer is:
$\frac{1}{\sqrt{5}}$
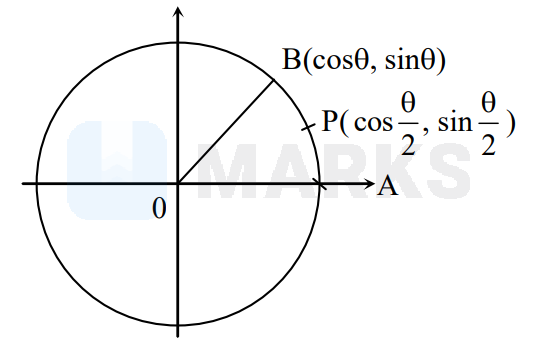
$\frac{\Delta(\mathrm{AOB})}{\Delta \mathrm{APB}}=2+\sqrt{5}$
$\frac{\cos \frac{\theta}{2}}{1-\cos \frac{\theta}{2}}=2+\sqrt{5} \quad \Rightarrow \cos \frac{\theta}{2}=\frac{1+\sqrt{5}}{4}$
So $\cos \theta=\frac{\sqrt{5}-1}{4}$
If $\theta \rightarrow 2 \theta$
$\frac{\Delta \mathrm{AOB}}{\Delta \mathrm{APB}}=\frac{\cos \theta}{1-\cos \theta}=\frac{1}{\sqrt{5}}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.