Search any question & find its solution
Question:
Answered & Verified by Expert
In a college, $40 \%$ students attend Mathematics class, 30\% students attend physics class and $20 \%$ students attend both the classes. If a student is chosen at random from the college, the probability that the student chosen attend only one class is
Options:
Solution:
1974 Upvotes
Verified Answer
The correct answer is:
$\frac{3}{10}$
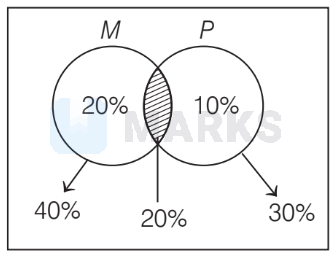
$\because$ Students in a college $=100 \%$
Let $P(M)$ be the probability who attend Maths class and $P(P)$ the probability who attend Physics classes.
$$
\therefore \quad P(M)=40 \%, \quad P(P)=30 \%
$$
$\therefore$ Probability of students who attend only Maths
$$
\begin{aligned}
\text { class } & =P(M)-P(M \cap P) \\
& =40 \%-20 \%=20 \%
\end{aligned}
$$
Probability of students who attend only Physics
$$
\begin{aligned}
\text { class } & =P(P)-P(M \cap P) \\
& =30 \%-20 \%=10 \%
\end{aligned}
$$
$\therefore$ Probability that the student chosen attend only one class $=20 \%+10 \%=30 \%$
$$
P=30 / 100=3 / 10
$$
Let $P(M)$ be the probability who attend Maths class and $P(P)$ the probability who attend Physics classes.

$$
\therefore \quad P(M)=40 \%, \quad P(P)=30 \%
$$
$\therefore$ Probability of students who attend only Maths
$$
\begin{aligned}
\text { class } & =P(M)-P(M \cap P) \\
& =40 \%-20 \%=20 \%
\end{aligned}
$$
Probability of students who attend only Physics
$$
\begin{aligned}
\text { class } & =P(P)-P(M \cap P) \\
& =30 \%-20 \%=10 \%
\end{aligned}
$$
$\therefore$ Probability that the student chosen attend only one class $=20 \%+10 \%=30 \%$
$$
P=30 / 100=3 / 10
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.