Search any question & find its solution
Question:
Answered & Verified by Expert
In a group of 70 people, 37 like coffee, 52 like tea and each person likes at least one of the two drinks. How many people like both coffee and tea?
Solution:
1463 Upvotes
Verified Answer
Let $C=$ Set of people who like coffee and $T=$ Set of people who like tea.
Then, $n(C \cup T)=70, n(C)=37$.
$n(T)=52, n(C \cap T)=\text { ? }$
Now, we know that
$\begin{aligned}
& n(C \cup T)=n(C)+n(T)-n(C \cap T) \\
\Rightarrow & 70=37+52-n(C \cap T) \\
\Rightarrow & n(C \cap T)=89-70=19
\end{aligned}$
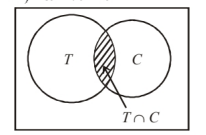
Hence, 19 people like both coffee and tea.
Then, $n(C \cup T)=70, n(C)=37$.
$n(T)=52, n(C \cap T)=\text { ? }$
Now, we know that
$\begin{aligned}
& n(C \cup T)=n(C)+n(T)-n(C \cap T) \\
\Rightarrow & 70=37+52-n(C \cap T) \\
\Rightarrow & n(C \cap T)=89-70=19
\end{aligned}$

Hence, 19 people like both coffee and tea.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.