Search any question & find its solution
Question:
Answered & Verified by Expert
In a photocell circuit the stopping potential, $V_{0}$, is a measure of the maximum kinetic energy of the photoelectrons. The following graph shows experimentally measured values of stopping potential versus frequency $v$ of incident light.
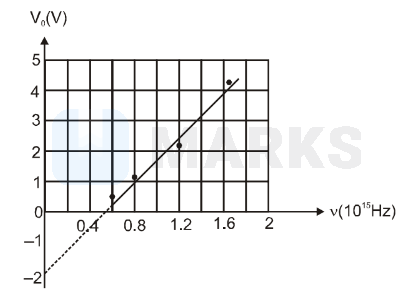
The values of Plank's constant and the work function as determined from the graph are (taking the magnitude of electronic charge to be $\left.\mathrm{e}=1.6 \times 10^{-19} \mathrm{C}\right)$
Options:

The values of Plank's constant and the work function as determined from the graph are (taking the magnitude of electronic charge to be $\left.\mathrm{e}=1.6 \times 10^{-19} \mathrm{C}\right)$
Solution:
1295 Upvotes
Verified Answer
The correct answer is:
$6.0 \times 10^{-34} \mathrm{Js}, 2.0 \mathrm{eV}$
$$
\mathrm{V}=\frac{\mathrm{hv}}{\mathrm{e}}-\phi
$$
Hence from graph $\phi=2 \mathrm{eV}$
$$
\begin{array}{l}
\frac{\mathrm{h}}{\mathrm{e}}=\mathrm{slope}=\frac{6}{1.6 \times 10^{15}} \\
\mathrm{~h}=\frac{6 \times 1.6 \times 10^{-19}}{1.6 \times 10^{15}}=6.0 \times 10^{-34}
\end{array}
$$
\mathrm{V}=\frac{\mathrm{hv}}{\mathrm{e}}-\phi
$$
Hence from graph $\phi=2 \mathrm{eV}$
$$
\begin{array}{l}
\frac{\mathrm{h}}{\mathrm{e}}=\mathrm{slope}=\frac{6}{1.6 \times 10^{15}} \\
\mathrm{~h}=\frac{6 \times 1.6 \times 10^{-19}}{1.6 \times 10^{15}}=6.0 \times 10^{-34}
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.