Search any question & find its solution
Question:
Answered & Verified by Expert
In a survey it was found that 21 people liked product $A$, 26 liked product $B$ and 29 liked product $C$. If 14 people liked products $A$ and $B, 12$ people liked products $C$ and $A, 14$ people liked products $B$ and $C$ and 8 liked all the three products. Find how many liked product $C$ only.
Solution:
1521 Upvotes
Verified Answer
$n(A \cap B)=14, n(A \cap C)=12$,
$n(B \cap C)=14$ and $n(A \cap B \cap C)=8$
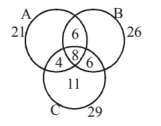
$n(C$ only $)=29-4-8-6=29-18=11$
$n(B \cap C)=14$ and $n(A \cap B \cap C)=8$

$n(C$ only $)=29-4-8-6=29-18=11$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.