Search any question & find its solution
Question:
Answered & Verified by Expert
In a \(\triangle A B C\) (shown in the figure below). State whether the following are true or false
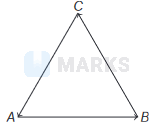
(i) \(\mathbf{A B}+\mathbf{B C}+\mathbf{C A}=\mathbf{0}\)
(ii) \(\mathbf{A B}+\mathbf{B C}-\mathbf{A C}=\mathbf{0}\)
(iii) \(\mathbf{A B}-\mathbf{C B}+\mathbf{C A}=\mathbf{0}\)
(iv) \(\mathbf{A B}+\mathbf{B C}-\mathbf{C A}=\mathbf{0}\)
Options:

(i) \(\mathbf{A B}+\mathbf{B C}+\mathbf{C A}=\mathbf{0}\)
(ii) \(\mathbf{A B}+\mathbf{B C}-\mathbf{A C}=\mathbf{0}\)
(iii) \(\mathbf{A B}-\mathbf{C B}+\mathbf{C A}=\mathbf{0}\)
(iv) \(\mathbf{A B}+\mathbf{B C}-\mathbf{C A}=\mathbf{0}\)
Solution:
2227 Upvotes
Verified Answer
The correct answer is:
(i) True (ii) True (iii) True (iv) False
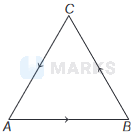
Following triangle came,
\(\begin{array}{llll}
& \mathbf{A B}+\mathbf{B C} =\mathbf{A C} \\
\Rightarrow & \mathbf{A B}+\mathbf{B C}+\mathbf{C A} =0 \quad \ldots (i) \\
\text {and } & \mathbf{A B}+\mathbf{B C}-\mathbf{A C} =0 \quad \ldots (ii) \\
\text {Also, } & \mathbf{C A}+\mathbf{A B} =\mathbf{C B} \\
\Rightarrow & \mathbf{C A}+\mathbf{A B}-\mathbf{C B} =0 \\
\text {or } & \mathbf{A B}-\mathbf{C B}+\mathbf{C A} =0 \quad \ldots (iii)
\end{array}\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.