Search any question & find its solution
Question:
Answered & Verified by Expert
In a triangle $A B C$, points $X$ and $Y$ are on $A B$ and $A C$, respectively, such that $X Y$ is parallel to BC, Which of the two following always hold? (Here [PQR] denotes the area of triangle PQR.)
(I) $[\mathrm{BCX}]=[\mathrm{BCY}]$
(II) $[\mathrm{ACX}] \cdot[\mathrm{ABY}]=[\mathrm{AXY}] \cdot[\mathrm{ABC}]$.
Options:
(I) $[\mathrm{BCX}]=[\mathrm{BCY}]$
(II) $[\mathrm{ACX}] \cdot[\mathrm{ABY}]=[\mathrm{AXY}] \cdot[\mathrm{ABC}]$.
Solution:
1383 Upvotes
Verified Answer
The correct answer is:
both (I) and (II)
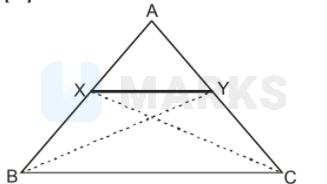
$\Delta \mathrm{BCX}=\Delta \mathrm{BCY}$ (Obvious)
Same base and same height
Now Let $\mathrm{A}(\overrightarrow{\mathrm{O}}), \overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{b}}, \quad \overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{c}}$
So $\overrightarrow{\mathrm{AX}}=\lambda \overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{AY}}=\lambda \overrightarrow{\mathrm{c}}$
$$
\Delta \mathrm{ACX}=\frac{1}{2} \lambda|\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}}|
$$
$$
\begin{array}{l}
\Delta \mathrm{ABY}=\frac{1}{2} \lambda|\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}}| \\
\Delta \mathrm{AXY}=\frac{1}{2} \lambda^{2}|\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}}| \\
\Delta \mathrm{ABC}=\frac{1}{2}|\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}}|
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.