Search any question & find its solution
Question:
Answered & Verified by Expert
In an isosceles trapezium, the length of one of the parallel sides, and the leng ths of the non-parallelsides are all equal to 30 . In order to maximize the area of the trapezium, the smallest angle should be
Options:
Solution:
2138 Upvotes
Verified Answer
The correct answer is:
$\frac{\pi}{3}$
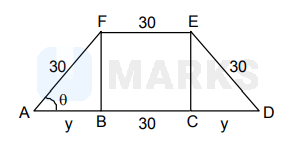
In $\triangle A B F, y=30 \cos \theta$
Area is $A=\frac{1}{2}[60+60 \cos \theta](30 \sin \theta)$
$\begin{array}{l}
=30(1+\cos \theta)(30 \sin \theta) \\
=900(\sin \theta+\sin \theta \cos \theta)
\end{array}$
For maximum or minimum
$\begin{array}{l}
\frac{d A}{d \theta}=900\left[\cos \theta+\left(-\sin ^{2} \theta+\cos ^{2} \theta\right)\right]=0 \\
\cos \theta-1+\cos ^{2} \theta+\cos ^{2} \theta=0 \\
2 \cos ^{2} \theta+\cos \theta-1=0 \\
(2 \cos \theta-1)(\cos \theta+1)=0
\end{array}$
$\cos \theta=\frac{1}{2}$ or $\cos \theta=-1$ (not possible) $\theta=60^{\circ}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.