Search any question & find its solution
Question:
Answered & Verified by Expert
In the arrangement shown in the figure, if the blocks of masses $m$ and $2 m$ are released from the state of rest, tension in the string is ( $\mu=$ coefficient of friction, string is massless and inextensible, pulley is frictionless)
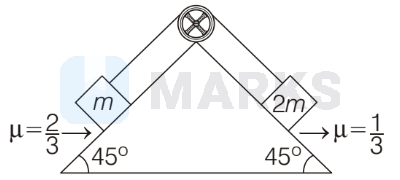
Options:

Solution:
2383 Upvotes
Verified Answer
The correct answer is:
$\frac{2 \sqrt{2} m g}{3}$
Let $N_1, N_2$ are normal reaction force and $f_1, f_2$ are the friction force on two blocks. acceleration is $a$ and tension is $T$.
The respective FBD
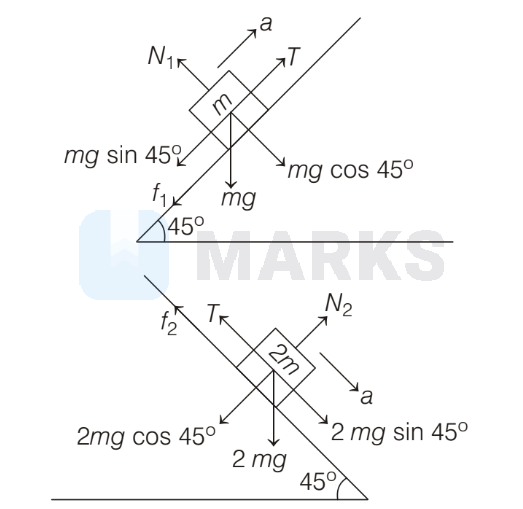
Friction force, $f_1=\mu N_1, f_2=\mu N_2$
As, $N_1=m g \cos 45^{\circ}, f_1=\frac{2}{3} \cdot m g \cos 45^{\circ}=\frac{\sqrt{2}}{3} m g$ and $N_2=2 m g \cos 45^{\circ}, f_2=\frac{2}{3} \cdot 2 m g \cos 45^{\circ}=\frac{2 \sqrt{2}}{3} m g$ $\Rightarrow$ Now, by second law of motion for $2 m$ mass, $2 m g \cos 45^{\circ}-T-f_2=2 m a$
$$
\sqrt{2} m g-T-\frac{2 \sqrt{2}}{3} m g=2 m a
$$
For $m_1, \quad T-f_1-m g \cos 45^{\circ}=m a$
$$
T-\frac{\sqrt{2}}{3} m g-\frac{m g}{\sqrt{2}}=m a
$$
Multiplying by 2 in Eq. (ii), we get
$$
2 T-\frac{2 \sqrt{2}}{3} m g-\sqrt{2} m g=2 m a
$$
Subtracting Eq. (iii) from Eq. (i), we get
$$
3 T-2 \sqrt{2} m g=0 \Rightarrow T=\frac{2 \sqrt{2} m g}{3}
$$
The respective FBD

Friction force, $f_1=\mu N_1, f_2=\mu N_2$
As, $N_1=m g \cos 45^{\circ}, f_1=\frac{2}{3} \cdot m g \cos 45^{\circ}=\frac{\sqrt{2}}{3} m g$ and $N_2=2 m g \cos 45^{\circ}, f_2=\frac{2}{3} \cdot 2 m g \cos 45^{\circ}=\frac{2 \sqrt{2}}{3} m g$ $\Rightarrow$ Now, by second law of motion for $2 m$ mass, $2 m g \cos 45^{\circ}-T-f_2=2 m a$
$$
\sqrt{2} m g-T-\frac{2 \sqrt{2}}{3} m g=2 m a
$$
For $m_1, \quad T-f_1-m g \cos 45^{\circ}=m a$
$$
T-\frac{\sqrt{2}}{3} m g-\frac{m g}{\sqrt{2}}=m a
$$
Multiplying by 2 in Eq. (ii), we get
$$
2 T-\frac{2 \sqrt{2}}{3} m g-\sqrt{2} m g=2 m a
$$
Subtracting Eq. (iii) from Eq. (i), we get
$$
3 T-2 \sqrt{2} m g=0 \Rightarrow T=\frac{2 \sqrt{2} m g}{3}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.