Search any question & find its solution
Question:
Answered & Verified by Expert
In the arrangement shown in the figure, work done by the string on the block of mass \(0.36 \mathrm{~kg}\) during the first second after the blocks are released from state of rest is (Ignore friction and mass of the string.)
(Acceleration due to gravity, \(g\) \(=10 \mathrm{~ms}^{-2}\))
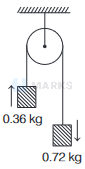
Options:
(Acceleration due to gravity, \(g\) \(=10 \mathrm{~ms}^{-2}\))

Solution:
1353 Upvotes
Verified Answer
The correct answer is:
\(8 \mathrm{~J}\)
According to the question,
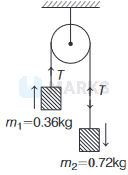
Given, mass of block \(1, m_1=0.36 \mathrm{~kg}\)
mass of block \(2, m_2=0.72 \mathrm{~kg}\)
and acceleration due to gravity, \(g=10 \mathrm{~m} / \mathrm{s}^2\)
Now, Dynamic equation of block \(m_1\left(m_2 > m_1\right)\).
\(\therefore \quad T-m_1 g=m_1 a\)...(i)
Dynamic equation of block \(m_2\left(m_2 > m_1\right)\).
\(\therefore \quad m_2 g-T=m_2 a \quad \ldots (ii)\)
Thus, from adding Eqs. (i) and (ii), we get
\(\therefore \quad T-m_1 g+m_2 g-T=m_1 a+m_2 a\)
\(m_2 g-m_1 g=a\left(m_1+m_2\right)\)
or
\(a=\frac{\left(m_2-m_1\right) g}{\left(m_1+m_2\right)}\)
Hence, acceleration, \(a=\left(\frac{m_2-m_1}{m_1+m_2}\right) g\)
\(\therefore\) Acceleration, \(a=\frac{(0.72-0.36)}{1.08} \times 10\)
\(a=\frac{3.6}{1.08} \mathrm{~m} / \mathrm{s}^2 \quad \ldots (iii)\)
Now, the tension force in the string is, for block 1st, \(m_1=0.36\)
\(\begin{aligned}
& T-m_1 g=m_1 a \\
& \frac{T-m_1 g}{m_1}=a \\
& \frac{T-3.6}{0.36}=\frac{3.6}{1.08} \\
& T=3.6+0.36 \times \frac{3.6}{1.08} \\
& T=4.8 \quad \ldots (iv)
\end{aligned}\)
Distance travelled by mass \(m_1\) block, By displacement-time relation, Displacement, \(s=u t+\frac{1}{2} \mathrm{at}^2\) \([\because u=0]\)
[by kinetic equation for uniformly motion]
\(s=\frac{1}{2} \times \frac{3.6}{1.08} \times(1)^2 \quad[\therefore t=1\) second given]
\(s=\frac{1}{2} \times \frac{3.6}{1.08}\)...(v)
Now, work done by the string on the block of mass \(\left(m_1\right)\) is \(0.36 \mathrm{~kg}\).
\(\therefore\) Work done, \(W=\) Tension force \((T) \times\) displacement \((s)\)
\(W=T \times \frac{1}{2} a t^2\)
From Eqs. (iv) and (v), we get
\(\begin{aligned}
& W=4.8 \times \frac{1}{2} \times \frac{3.6}{1.08} \\
& W=\frac{16}{2} \Rightarrow W=8 \mathrm{~J}
\end{aligned}\)

Given, mass of block \(1, m_1=0.36 \mathrm{~kg}\)
mass of block \(2, m_2=0.72 \mathrm{~kg}\)
and acceleration due to gravity, \(g=10 \mathrm{~m} / \mathrm{s}^2\)
Now, Dynamic equation of block \(m_1\left(m_2 > m_1\right)\).
\(\therefore \quad T-m_1 g=m_1 a\)...(i)
Dynamic equation of block \(m_2\left(m_2 > m_1\right)\).
\(\therefore \quad m_2 g-T=m_2 a \quad \ldots (ii)\)
Thus, from adding Eqs. (i) and (ii), we get
\(\therefore \quad T-m_1 g+m_2 g-T=m_1 a+m_2 a\)
\(m_2 g-m_1 g=a\left(m_1+m_2\right)\)
or
\(a=\frac{\left(m_2-m_1\right) g}{\left(m_1+m_2\right)}\)
Hence, acceleration, \(a=\left(\frac{m_2-m_1}{m_1+m_2}\right) g\)
\(\therefore\) Acceleration, \(a=\frac{(0.72-0.36)}{1.08} \times 10\)
\(a=\frac{3.6}{1.08} \mathrm{~m} / \mathrm{s}^2 \quad \ldots (iii)\)
Now, the tension force in the string is, for block 1st, \(m_1=0.36\)
\(\begin{aligned}
& T-m_1 g=m_1 a \\
& \frac{T-m_1 g}{m_1}=a \\
& \frac{T-3.6}{0.36}=\frac{3.6}{1.08} \\
& T=3.6+0.36 \times \frac{3.6}{1.08} \\
& T=4.8 \quad \ldots (iv)
\end{aligned}\)
Distance travelled by mass \(m_1\) block, By displacement-time relation, Displacement, \(s=u t+\frac{1}{2} \mathrm{at}^2\) \([\because u=0]\)
[by kinetic equation for uniformly motion]
\(s=\frac{1}{2} \times \frac{3.6}{1.08} \times(1)^2 \quad[\therefore t=1\) second given]
\(s=\frac{1}{2} \times \frac{3.6}{1.08}\)...(v)
Now, work done by the string on the block of mass \(\left(m_1\right)\) is \(0.36 \mathrm{~kg}\).
\(\therefore\) Work done, \(W=\) Tension force \((T) \times\) displacement \((s)\)
\(W=T \times \frac{1}{2} a t^2\)
From Eqs. (iv) and (v), we get
\(\begin{aligned}
& W=4.8 \times \frac{1}{2} \times \frac{3.6}{1.08} \\
& W=\frac{16}{2} \Rightarrow W=8 \mathrm{~J}
\end{aligned}\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.