Search any question & find its solution
Question:
Answered & Verified by Expert
In the circuit given below, if the bulb is to glow with maximum intensity, the value of ' $R$ ' is
(neglect internal resistance of the cell)
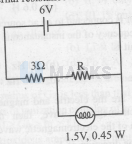
Options:
(neglect internal resistance of the cell)

Solution:
1941 Upvotes
Verified Answer
The correct answer is:
$1.25 \Omega$
Resistance of bulb, $R=\frac{V^2}{P}$
$=\frac{(1.5)^2}{0.45}=5 \Omega$
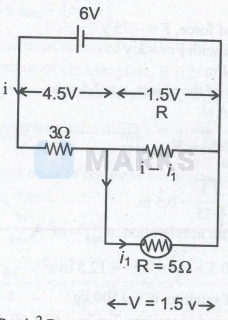
$P=i_1^2 R$
$\begin{aligned} & 0.45=\mathrm{i}_1{ }^2 5 \\ & \mathrm{i}_1=0.3 \mathrm{~A}\end{aligned}$
Apply KVL, We have
$\begin{aligned} & -6+3 \mathrm{i} 1.5=0 \\ & \mathrm{i}=\frac{6-1.5}{3}=1.5 \mathrm{~A} \\ & 1.5=\left(\mathrm{i}-\mathrm{i}_1\right) \mathrm{R} \\ & 1.5=(1.5-0.3) \mathrm{R} \\ & \mathrm{R}=\frac{1.5}{1.2}=1.25 \Omega\end{aligned}$
$=\frac{(1.5)^2}{0.45}=5 \Omega$

$P=i_1^2 R$
$\begin{aligned} & 0.45=\mathrm{i}_1{ }^2 5 \\ & \mathrm{i}_1=0.3 \mathrm{~A}\end{aligned}$
Apply KVL, We have
$\begin{aligned} & -6+3 \mathrm{i} 1.5=0 \\ & \mathrm{i}=\frac{6-1.5}{3}=1.5 \mathrm{~A} \\ & 1.5=\left(\mathrm{i}-\mathrm{i}_1\right) \mathrm{R} \\ & 1.5=(1.5-0.3) \mathrm{R} \\ & \mathrm{R}=\frac{1.5}{1.2}=1.25 \Omega\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.