Search any question & find its solution
Question:
Answered & Verified by Expert
In the circuit shown, the AC source has voltage $\mathrm{V}=20 \cos (\omega \mathrm{t})$ volt with $\omega=2000 \mathrm{rad} / \mathrm{s}$. The magnitude of amplitude current will be nearly
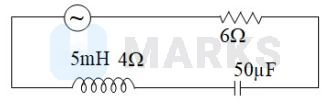
Options:
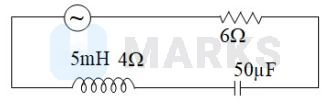
Solution:
2448 Upvotes
Verified Answer
The correct answer is:
3.3 A
Current through the circuit is given by
$i=\frac{V_0}{\sqrt{R^2+\left(X_C-X_L\right)^2}}$ where $X_L=\omega L$ and $X C=\frac{1}{\omega C}$.
Given: $\mathrm{V}_0=20 \mathrm{~V},=6 \Omega, \mathrm{L}=5 \times 10^{-3} \mathrm{H}, \omega=2000 \frac{\mathrm{rad}}{\mathrm{s}}$ and $\mathrm{C}=50 \times 10^{-6} \mathrm{~F}$
$\begin{aligned}
& \therefore \mathrm{X}_{\mathrm{C}}=\frac{1}{50 \times 10^{-6} \times 2000} \Omega 10 \Omega \text { and } \mathrm{X}_{\mathrm{L}}=2000 \times 5 \times 10^{-3} \Omega=10 \Omega \\
& \because \mathrm{X}_{\mathrm{C}}=\mathrm{X}_{\mathrm{L}}
\end{aligned}$
The current is simply: $\mathrm{I}=\frac{\mathrm{v}_0}{\mathrm{R}}$
$\therefore \mathrm{i}=\frac{20}{6} \mathrm{~A}=3.3 \mathrm{~A}$
$i=\frac{V_0}{\sqrt{R^2+\left(X_C-X_L\right)^2}}$ where $X_L=\omega L$ and $X C=\frac{1}{\omega C}$.
Given: $\mathrm{V}_0=20 \mathrm{~V},=6 \Omega, \mathrm{L}=5 \times 10^{-3} \mathrm{H}, \omega=2000 \frac{\mathrm{rad}}{\mathrm{s}}$ and $\mathrm{C}=50 \times 10^{-6} \mathrm{~F}$
$\begin{aligned}
& \therefore \mathrm{X}_{\mathrm{C}}=\frac{1}{50 \times 10^{-6} \times 2000} \Omega 10 \Omega \text { and } \mathrm{X}_{\mathrm{L}}=2000 \times 5 \times 10^{-3} \Omega=10 \Omega \\
& \because \mathrm{X}_{\mathrm{C}}=\mathrm{X}_{\mathrm{L}}
\end{aligned}$
The current is simply: $\mathrm{I}=\frac{\mathrm{v}_0}{\mathrm{R}}$
$\therefore \mathrm{i}=\frac{20}{6} \mathrm{~A}=3.3 \mathrm{~A}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.