Search any question & find its solution
Question:
Answered & Verified by Expert
In the circuit shown, the current through the $4 \Omega$ resistor is $1 \mathrm{~A}$ when the points $P$ and $M$ are connected to a DC voltage source. The potential difference between the points $M$ and $N$ is
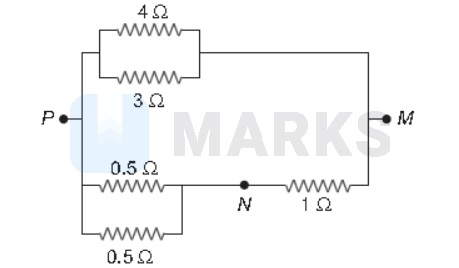
Options:

Solution:
1035 Upvotes
Verified Answer
The correct answer is:
$3.2 \mathrm{~V}$
Key Idea : In parallel resistances, potential difference across them is same.
Potential difference across PM
$V=4 \times 1=4 \text { volt (ie, across } 4 \Omega)$
Equivalent resistance of lower side arm,
$R_{e q}=1+\frac{0.5 \times 0.5}{0.5+0.5}=1.25 \Omega$
Now the circuit can be shown as
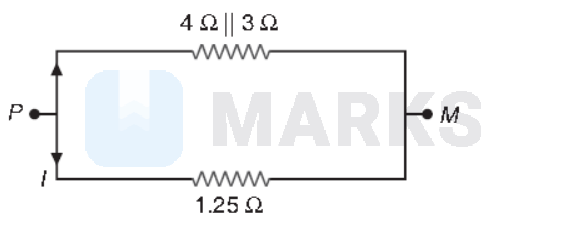
Let current I flows in lower branch, so
$\begin{aligned}
1.25 I & =4 \mathrm{~V} \\
I & =\frac{4}{1.25}=3.2 \mathrm{~A}
\end{aligned}$
Therefore, 3.2 A current flows in $1 \Omega$ resistance, hence potential difference between $M$ and $N$ is
$V^{\prime}=3.2 \times 1=3.2$ volt
Potential difference across PM
$V=4 \times 1=4 \text { volt (ie, across } 4 \Omega)$
Equivalent resistance of lower side arm,
$R_{e q}=1+\frac{0.5 \times 0.5}{0.5+0.5}=1.25 \Omega$
Now the circuit can be shown as

Let current I flows in lower branch, so
$\begin{aligned}
1.25 I & =4 \mathrm{~V} \\
I & =\frac{4}{1.25}=3.2 \mathrm{~A}
\end{aligned}$
Therefore, 3.2 A current flows in $1 \Omega$ resistance, hence potential difference between $M$ and $N$ is
$V^{\prime}=3.2 \times 1=3.2$ volt
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.